Hvordan multiplisere en brøk med et naturlig tall. IX. Refleksjon over læringsaktiviteter i klasserommet. Multiplisere en vanlig brøk med en vanlig brøk

§ 87. Addisjon av brøker.

Å legge til brøker har mange likheter med å legge til hele tall. Addisjon av brøker er en handling som består i at flere gitte tall (ledd) kombineres til ett tall (sum), som inneholder alle enhetene og brøkene av enhetene til leddene.

Vi vil vurdere tre saker sekvensielt:

1. Addisjon av brøker med like nevnere.
2. Addisjon av brøker med ulike nevnere.
3. Addisjon av blandede tall.

1. Addisjon av brøker med like nevnere.

Tenk på et eksempel: 1/5 + 2/5.

La oss ta segment AB (fig. 17), ta det som ett og dele det i 5 like deler, så vil del AC av dette segmentet være lik 1/5 av segment AB, og en del av samme segment CD vil være lik 2/5 AB.

Fra tegningen er det klart at hvis vi tar segmentet AD, vil det være lik 3/5 AB; men segmentet AD er nøyaktig summen av segmentene AC og CD. Så vi kan skrive:

1 / 5 + 2 / 5 = 3 / 5

Med tanke på disse begrepene og den resulterende summen, ser vi at telleren av summen ble oppnådd ved å legge til tellerne til begrepene, og nevneren forble uendret.

Fra dette får vi følgende regel: For å legge til brøker med de samme nevnerne, må du legge til deres tellere og la den samme nevneren være igjen.

La oss se på et eksempel:

2. Addisjon av brøker med ulike nevnere.

La oss legge til brøkene: 3 / 4 + 3 / 8 Først må de reduseres til laveste fellesnevner:

Mellomlenken 6/8 + 3/8 kunne ikke skrives; vi har skrevet det her for klarhet.

For å legge til brøker med ulike nevnere, må du derfor først redusere dem til laveste fellesnevner, legge til tellerne og merke fellesnevneren.

La oss vurdere et eksempel (vi vil skrive tilleggsfaktorer over de tilsvarende brøkene):

3. Addisjon av blandede tall.

La oss legge til tallene: 2 3/8 + 3 5/6.

La oss først bringe brøkdelene av tallene våre til en fellesnevner og skrive dem om igjen:

Nå legger vi til heltalls- og brøkdelene sekvensielt:

§ 88. Subtraksjon av brøker.

Å subtrahere brøker er definert på samme måte som å trekke fra hele tall. Dette er en handling som, gitt summen av to ledd og ett av dem, finner et annet ledd. La oss vurdere tre saker etter hverandre:

1. Trekk fra brøker med like nevnere.
2. Subtrahere brøker med ulike nevnere.
3. Subtraksjon av blandede tall.

1. Trekk fra brøker med like nevnere.

La oss se på et eksempel:

13 / 15 - 4 / 15

La oss ta segmentet AB (fig. 18), ta det som en enhet og dele det i 15 like deler; da vil del AC av dette segmentet representere 1/15 av AB, og del AD av samme segment vil tilsvare 13/15 AB. La oss sette til side et annet segment ED lik 4/15 AB.

Vi må trekke fra brøken 4/15 fra 13/15. På tegningen betyr dette at segment ED må trekkes fra segment AD. Som et resultat vil segment AE forbli, som er 9/15 av segment AB. Så vi kan skrive:

Eksemplet vi laget viser at telleren til forskjellen ble oppnådd ved å trekke fra tellerne, men nevneren forble den samme.

Derfor, for å trekke fra brøker med like nevnere, må du trekke fra telleren til subtrahenden fra telleren til minuenden og la den samme nevneren være igjen.

2. Subtrahere brøker med ulike nevnere.

Eksempel. 3/4 - 5/8

La oss først redusere disse brøkene til laveste fellesnevner:

Den mellomliggende 6 / 8 - 5 / 8 er skrevet her for klarhet, men kan hoppes over senere.

For å trekke en brøk fra en brøk, må du derfor først redusere dem til laveste fellesnevner, deretter trekke fra telleren til minuenden fra telleren til minuenden og signere fellesnevneren under deres differanse.

La oss se på et eksempel:

3. Subtraksjon av blandede tall.

Eksempel. 10 3/4 - 7 2/3.

La oss redusere brøkdelene av minuend og subtrahend til laveste fellesnevner:

Vi trakk en helhet fra en helhet og en brøk fra en brøk. Men det er tilfeller der brøkdelen av subtrahenden er større enn brøkdelen av minuenden. I slike tilfeller må du ta en enhet fra hele delen av minuenden, dele den opp i de delene der brøkdelen er uttrykt, og legge den til brøkdelen av minuenden. Og så vil subtraksjonen utføres på samme måte som i forrige eksempel:

§ 89. Multiplikasjon av brøker.

Når vi studerer brøkmultiplikasjon vil vi vurdere neste spørsmål:

1. Multiplisere en brøk med et helt tall.
2. Finne brøkdelen av et gitt tall.
3. Multiplisere et helt tall med en brøk.
4. Multiplisere en brøk med en brøk.
5. Multiplikasjon av blandede tall.
6. Rentebegrepet.
7. Finne prosentandelen av et gitt tall. La oss vurdere dem sekvensielt.

1. Multiplisere en brøk med et helt tall.

Å multiplisere en brøk med et helt tall har samme betydning som å multiplisere et helt tall med et heltall. Å multiplisere en brøk (multiplikand) med et heltall (faktor) betyr å lage en sum av identiske ledd, der hvert ledd er lik multiplikanden, og antall ledd er lik multiplikatoren.

Dette betyr at hvis du trenger å multiplisere 1/9 med 7, så kan det gjøres slik:

Vi fikk enkelt resultatet, siden handlingen ble redusert til å legge til brøker med samme nevnere. Derfor,

Betraktning av denne handlingen viser at å multiplisere en brøk med et helt tall tilsvarer å øke denne brøken like mange ganger som det er enheter i hele tallet. Og siden økende en brøk oppnås enten ved å øke telleren

eller ved å redusere nevneren , så kan vi enten multiplisere telleren med et heltall eller dele nevneren på det, hvis slik divisjon er mulig.

Herfra får vi regelen:

For å multiplisere en brøk med et helt tall, multipliserer du telleren med det hele tallet og lar nevneren være den samme, eller, hvis mulig, deler du nevneren på det tallet, og lar telleren være uendret.

Når du multipliserer, er forkortelser mulig, for eksempel:

2. Finne brøkdelen av et gitt tall. Det er mange problemer der du må finne, eller beregne, en del av et gitt tall. Forskjellen mellom disse problemene og andre er at de gir antall objekter eller måleenheter, og du må finne en del av dette tallet, som også er angitt her med en viss brøkdel. For å lette forståelsen vil vi først gi eksempler på slike problemer, og deretter introdusere en metode for å løse dem.

Oppgave 1. Jeg hadde 60 rubler; Jeg brukte 1/3 av disse pengene på å kjøpe bøker. Hvor mye kostet bøkene?

Oppgave 2. Toget skal kjøre en avstand mellom byer A og B lik 300 km. Han har allerede tilbakelagt 2/3 av denne distansen. Hvor mange kilometer er dette?

Oppgave 3. Det er 400 hus i landsbyen, 3/4 av dem er murstein, resten er av tre. Hvor mange murhus er det totalt?

Dette er noen av de mange problemene vi møter for å finne en del av et gitt tall. De kalles vanligvis problemer for å finne brøkdelen av et gitt tall.

Løsning på oppgave 1. Fra 60 gni. Jeg brukte 1/3 på bøker; Dette betyr at for å finne prisen på bøker må du dele tallet 60 på 3:

Løse oppgave 2. Poenget med problemet er at du må finne 2/3 av 300 km. La oss først beregne 1/3 av 300; dette oppnås ved å dele 300 km med 3:

300: 3 = 100 (det er 1/3 av 300).

For å finne to tredjedeler av 300, må du doble den resulterende kvotienten, dvs. multiplisere med 2:

100 x 2 = 200 (det er 2/3 av 300).

Løse problem 3. Her må du bestemme antall murhus som utgjør 3/4 av 400. La oss først finne 1/4 av 400,

400: 4 = 100 (det er 1/4 av 400).

For å beregne tre fjerdedeler av 400, må den resulterende kvotienten tredobles, dvs. multiplisert med 3:

100 x 3 = 300 (det er 3/4 av 400).

Basert på løsningen på disse problemene kan vi utlede følgende regel:

For å finne verdien av en brøk fra et gitt tall, må du dele dette tallet med nevneren til brøken og multiplisere den resulterende kvotienten med telleren.

3. Multiplisere et helt tall med en brøk.

Tidligere (§ 26) ble det slått fast at multiplikasjon av heltall skulle forstås som addisjon av identiske ledd (5 x 4 = 5+5 +5+5 = 20). I dette avsnittet (punkt 1) ble det fastslått at å multiplisere en brøk med et heltall betyr å finne summen av identiske ledd lik denne brøken.

I begge tilfeller besto multiplikasjon i å finne summen av identiske ledd.

Nå går vi videre til å multiplisere et helt tall med en brøk. Her vil vi for eksempel møte multiplikasjon: 9 2 / 3. Det er klart at den tidligere definisjonen av multiplikasjon ikke gjelder for dette tilfellet. Dette fremgår av det faktum at vi ikke kan erstatte en slik multiplikasjon ved å legge til like tall.

På grunn av dette må vi gi en ny definisjon av multiplikasjon, det vil si, med andre ord, svare på spørsmålet om hva som skal forstås ved multiplikasjon med en brøk, hvordan denne handlingen skal forstås.

Betydningen av å multiplisere et helt tall med en brøk er tydelig fra følgende definisjon: å multiplisere et heltall (multiplikand) med en brøk (multiplikand) betyr å finne denne brøkdelen av multiplikanden.

Å multiplisere 9 med 2/3 betyr nemlig å finne 2/3 av ni enheter. I forrige avsnitt ble slike problemer løst; så det er lett å finne ut at vi ender opp med 6.

Men nå er det en interessant og viktig spørsmål: hvorfor er de slik ved første øyekast? ulike handlinger Hvordan er det å finne summen av like tall og finne brøkdelen av et tall kalt med det samme ordet «multiplikasjon» i aritmetikk?

Dette skjer fordi den forrige handlingen (gjenta tallet med ledd flere ganger) og den nye handlingen (finne brøkdelen av tallet) gir svaret på homogene spørsmål. Det betyr at vi her går ut fra betraktningene om at homogene spørsmål eller oppgaver løses ved samme handling.

For å forstå dette, vurder følgende problem: "1 m tøy koster 50 rubler. Hvor mye vil 4 m slikt tøy koste?

Dette problemet løses ved å multiplisere antall rubler (50) med antall meter (4), dvs. 50 x 4 = 200 (rubler).

La oss ta det samme problemet, men i det vil mengden tøy bli uttrykt som en brøkdel: "1 m tøy koster 50 rubler. Hvor mye vil 3/4 m av et slikt tøy koste?"

Dette problemet må også løses ved å multiplisere antall rubler (50) med antall meter (3/4).

Du kan endre tallene i den flere ganger, uten å endre betydningen av problemet, for eksempel ta 9/10 m eller 2 3/10 m, etc.

Siden disse problemene har samme innhold og bare er forskjellige i tall, kaller vi handlingene som brukes for å løse dem det samme ordet - multiplikasjon.

Hvordan multipliserer du et helt tall med en brøk?

La oss ta tallene som ble funnet i den siste oppgaven:

I følge definisjonen må vi finne 3/4 av 50. La oss først finne 1/4 av 50, og deretter 3/4.

1/4 av 50 er 50/4;

3/4 av tallet 50 er .

Derfor.

La oss se på et annet eksempel: 12 5 / 8 =?

1/8 av tallet 12 er 12/8,

5/8 av tallet 12 er .

Derfor,

Herfra får vi regelen:

For å multiplisere et helt tall med en brøk, må du multiplisere hele tallet med telleren til brøken og gjøre dette produktet til telleren, og signere nevneren til denne brøken som nevneren.

La oss skrive denne regelen med bokstaver:

For å gjøre denne regelen helt klar, bør det huskes at en brøk kan betraktes som en kvotient. Derfor er det nyttig å sammenligne den funnet regelen med regelen for å multiplisere et tall med en kvotient, som ble angitt i § 38

Det er viktig å huske at før du utfører multiplikasjon, bør du gjøre (hvis mulig) reduksjoner, For eksempel:

4. Multiplisere en brøk med en brøk.Å multiplisere en brøk med en brøk har samme betydning som å multiplisere et helt tall med en brøk, det vil si at når du multipliserer en brøk med en brøk, må du finne brøken som er i faktoren fra den første brøken (multipikanet).

Å multiplisere 3/4 med 1/2 (halvparten) betyr nemlig å finne halvparten av 3/4.

Hvordan multipliserer du en brøk med en brøk?

La oss ta et eksempel: 3/4 multiplisert med 5/7. Dette betyr at du må finne 5/7 av 3/4. La oss først finne 1/7 av 3/4, og deretter 5/7

1/7 av tallet 3/4 vil bli uttrykt som følger:

5/7 tall 3/4 vil bli uttrykt som følger:

Dermed,

Et annet eksempel: 5/8 multiplisert med 4/9.

1/9 av 5/8 er ,

4/9 av tallet 5/8 er .

Dermed,

Fra disse eksemplene kan følgende regel utledes:

For å multiplisere en brøk med en brøk, må du multiplisere telleren med telleren, og nevneren med nevneren, og gjøre det første produktet til telleren, og det andre produktet til nevneren av produktet.

Dette er regelen i generelt syn kan skrives slik:

Ved multiplikasjon er det nødvendig å foreta (om mulig) reduksjoner. La oss se på eksempler:

5. Multiplikasjon av blandede tall. Siden blandede tall lett kan erstattes med uekte brøker, brukes denne omstendigheten vanligvis når man multipliserer blandede tall. Dette betyr at i tilfeller hvor multiplikatoren, eller multiplikatoren, eller begge faktorene er uttrykt som blandede tall, erstattes de med uekte brøker. La oss multiplisere, for eksempel, blandede tall: 2 1/2 og 3 1/5. La oss gjøre hver av dem til en uekte brøk og deretter multiplisere de resulterende brøkene i henhold til regelen for å multiplisere en brøk med en brøk:

Regel. For å multiplisere blandede tall, må du først konvertere dem til uekte brøker og deretter multiplisere dem i henhold til regelen for å multiplisere brøker med brøker.

Merk. Hvis en av faktorene er et heltall, kan multiplikasjonen utføres basert på fordelingsloven som følger:

6. Rentebegrepet. Når vi løser oppgaver og utfører ulike praktiske beregninger, bruker vi alle slags brøker. Men det må huskes at mange mengder tillater ikke bare noen, men naturlige inndelinger for dem. For eksempel kan du ta en hundredel (1/100) av en rubel, det vil være en kopek, to hundredeler er 2 kopek, tre hundredeler er 3 kopek. Du kan ta 1/10 av en rubel, det vil være "10 kopek, eller en ti-kopek-bit. Du kan ta en fjerdedel av en rubel, dvs. 25 kopek, en halv rubel, dvs. 50 kopek (femti kopek). Men de tar det praktisk talt ikke, for eksempel 2/7 av en rubel fordi rubelen ikke er delt inn i syvendedeler.

Vektenheten, det vil si kilogrammet, tillater først og fremst desimaldelinger, for eksempel 1/10 kg, eller 100 g. Og slike brøkdeler av et kilo som 1/6, 1/11, 1/13 er ikke vanlige.

Generelt er våre (metriske) mål desimaler og tillater desimalinndelinger.

Det skal imidlertid bemerkes at det er ekstremt nyttig og praktisk i en lang rekke tilfeller å bruke den samme (uniforme) metoden for å dele opp mengder. Mange års erfaring har vist at en så godt begrunnet deling er den "hundrede" divisjonen. La oss vurdere flere eksempler knyttet til de mest forskjellige områdene av menneskelig praksis.

1. Prisen på bøker har gått ned med 12/100 av forrige pris.

Eksempel. Den forrige prisen på boken var 10 rubler. Det gikk ned med 1 rubel. 20 kopek

2. Sparebanker betaler innskytere 2/100 av innskuddsbeløpet for sparing i løpet av året.

Eksempel. 500 rubler er satt inn i kassaapparatet, inntekten fra dette beløpet for året er 10 rubler.

3. Antall uteksaminerte fra én skole var 5/100 av totalt antall elever.

EKSEMPEL Det var bare 1200 elever ved skolen, hvorav 60 ble uteksaminert.

Hundredelen av et tall kalles en prosentandel.

Ordet "prosent" er lånt fra latinsk språk og roten "cent" betyr hundre. Sammen med preposisjonen (pro centum) betyr dette ordet "for hundre." Betydningen av et slikt uttrykk følger av det faktum at innledningsvis i antikkens Roma renter var pengene som skyldneren betalte til utlåneren «for hvert hundre». Ordet "cent" høres i slike kjente ord: centner (hundre kilo), centimeter (si centimeter).

For eksempel, i stedet for å si at i løpet av den siste måneden produserte anlegget 1/100 av alle produkter produsert av det var defekte, vil vi si dette: I løpet av den siste måneden produserte anlegget én prosent av defektene. I stedet for å si: anlegget produserte 4/100 flere produkter enn den fastsatte planen, vil vi si: anlegget overskred planen med 4 prosent.

Eksemplene ovenfor kan uttrykkes annerledes:

1. Prisen på bøker har gått ned med 12 prosent av forrige pris.

2. Sparebanker betaler innskytere 2 prosent per år av innskuddsbeløpet på sparepenger.

3. Antall uteksaminerte fra én skole var 5 prosent av alle skoleelever.

For å forkorte bokstaven er det vanlig å skrive %-symbolet i stedet for ordet "prosent".

Du må imidlertid huske at i beregninger skrives vanligvis ikke %-tegnet, det kan skrives i problemstillingen og i sluttresultatet. Når du utfører beregninger, må du skrive en brøk med en nevner på 100 i stedet for et helt tall med dette symbolet.

Du må kunne erstatte et heltall med det angitte ikonet med en brøkdel med en nevner på 100:

Omvendt må du venne deg til å skrive et heltall med det angitte symbolet i stedet for en brøk med en nevner på 100:

7. Finne prosentandelen av et gitt tall.

Oppgave 1. Skolen fikk 200 kubikkmeter. m ved, med bjørkeved som utgjør 30 %. Hvor mye bjørkeved var det?

Meningen med denne oppgaven er at bjørkeved bare utgjorde en del av veden som ble levert til skolen, og denne delen er uttrykt i brøken 30/100. Dette betyr at vi har en oppgave å finne en brøkdel av et tall. For å løse det må vi multiplisere 200 med 30/100 (problemer med å finne brøken av et tall løses ved å multiplisere tallet med brøken.).

Dette betyr at 30 % av 200 tilsvarer 60.

Fraksjonen 30/100 som oppstår i denne oppgaven kan reduseres med 10. Det ville være mulig å gjøre denne reduksjonen helt fra begynnelsen; løsningen på problemet ville ikke ha endret seg.

Oppgave 2. Det var 300 barn i ulike aldre i leiren. Barn 11 år utgjorde 21 %, barn 12 år utgjorde 61 % og til slutt 13 år gamle barn utgjorde 18 %. Hvor mange barn i hver alder var det i leiren?

I denne oppgaven må du utføre tre beregninger, dvs. finne antall barn 11 år gamle, deretter 12 år og til slutt 13 år gamle.

Dette betyr at her må du finne brøkdelen av tallet tre ganger. La oss gjøre det:

1) Hvor mange 11 år gamle barn var det?

2) Hvor mange 12 år gamle barn var det?

3) Hvor mange 13 år gamle barn var det?

Etter å ha løst problemet, er det nyttig å legge til tallene som er funnet; summen deres skal være 300:

63 + 183 + 54 = 300

Det bør også bemerkes at summen av prosentene gitt i problemstillingen er 100:

21% + 61% + 18% = 100%

Dette tyder på det totalt antall barn i leiren ble tatt som 100 %.

3 a d a h a 3. Arbeideren mottok 1200 rubler per måned. Av dette brukte han 65 % på mat, 6 % på leiligheter og oppvarming, 4 % på gass, elektrisitet og radio, 10 % på kulturelle behov og 15 % spart. Hvor mye penger ble brukt på behovene angitt i oppgaven?

For å løse dette problemet må du finne brøkdelen av 1200 5 ganger. La oss gjøre dette.

1) Hvor mye penger ble brukt på mat? Problemet sier at denne utgiften er 65 % av den totale inntekten, dvs. 65/100 av tallet 1200. La oss regne ut:

2) Hvor mye betalte du for en leilighet med oppvarming? På samme måte som den forrige, kommer vi til følgende beregning:

3) Hvor mye betalte du for gass, strøm og radio?

4) Hvor mye penger ble brukt på kulturelle behov?

5) Hvor mye penger sparte arbeideren?

For å sjekke er det nyttig å legge sammen tallene som finnes i disse 5 spørsmålene. Beløpet skal være 1200 rubler. All inntjening tas som 100 %, noe som er enkelt å sjekke ved å legge sammen prosenttallene som er gitt i problemstillingen.

Vi løste tre problemer. Til tross for at disse problemene handlet om forskjellige ting (levering av ved til skolen, antall barn i ulike aldre, arbeiderens utgifter), ble de løst på samme måte. Dette skjedde fordi det i alle problemer var nødvendig å finne flere prosent av gitte tall.

§ 90. Brøkdeling.

Når vi studerer brøkdeling, vil vi vurdere følgende spørsmål:

1. Del et heltall med et heltall.
2. Å dele en brøk på et helt tall
3. Å dele et helt tall på en brøk.
4. Å dele en brøk på en brøk.
5. Deling av blandede tall.
6. Finne et tall fra den gitte brøken.
7. Finne et tall etter prosentandelen.

La oss vurdere dem sekvensielt.

1. Del et heltall med et heltall.

Som det ble indikert i avdelingen for heltall, er divisjon handlingen som består i det faktum at gitt produktet av to faktorer (dividende) og en av disse faktorene (divisor), finnes en annen faktor.

Vi så på å dele et heltall med et heltall i delen om heltall. Vi møtte to tilfeller av deling der: divisjon uten en rest, eller "helt" (150: 10 = 15), og divisjon med en rest (100: 9 = 11 og 1 rest). Vi kan derfor si at når det gjelder heltall, er nøyaktig deling ikke alltid mulig, fordi utbyttet ikke alltid er produktet av divisor med heltall. Etter å ha introdusert multiplikasjon med en brøk, kan vi vurdere ethvert tilfelle av å dele heltall mulig (bare divisjon med null er ekskludert).

For eksempel betyr å dele 7 med 12 å finne et tall hvis produkt med 12 vil være lik 7. Et slikt tall er brøken 7 / 12 fordi 7 / 12 12 = 7. Et annet eksempel: 14: 25 = 14 / 25, fordi 14 / 25 25 = 14.

For å dele et helt tall med et helt tall, må du derfor lage en brøk hvis teller er lik utbyttet og nevneren er lik divisor.

2. Å dele en brøk på et helt tall.

Del brøken 6 / 7 med 3. I henhold til definisjonen av divisjon gitt ovenfor, har vi her produktet (6 / 7) og en av faktorene (3); det kreves å finne en andre faktor som, multiplisert med 3, vil gi det gitte produktet 6/7. Det skal selvsagt være tre ganger mindre enn dette produktet. Dette betyr at oppgaven som ble lagt foran oss var å redusere brøken 6/7 med 3 ganger.

Vi vet allerede at å redusere en brøk kan gjøres enten ved å redusere telleren eller øke nevneren. Derfor kan du skrive:

I dette tilfellet er telleren 6 delelig med 3, så telleren bør reduseres med 3 ganger.

La oss ta et annet eksempel: 5 / 8 delt på 2. Her er ikke telleren 5 delelig med 2, noe som betyr at nevneren må multipliseres med dette tallet:

Basert på dette kan en regel lages: For å dele en brøk på et helt tall, må du dele telleren til brøken på det hele tallet.(hvis mulig), forlater den samme nevneren, eller multipliser nevneren til brøken med dette tallet, og forlater den samme telleren.

3. Å dele et helt tall på en brøk.

La det være nødvendig å dele 5 på 1/2, dvs. finne et tall som etter å ha multiplisert med 1/2 vil gi produktet 5. Dette tallet må selvsagt være større enn 5, siden 1/2 er en egen brøk , og når du multipliserer et tall, må produktet av en egenbrøk være mindre enn produktet som multipliseres. For å gjøre dette klarere, la oss skrive handlingene våre som følger: 5: 1 / 2 = X , som betyr x 1/2 = 5.

Vi må finne et slikt tall X , som, hvis multiplisert med 1/2, ville gi 5. Siden å multiplisere et bestemt tall med 1/2 betyr å finne 1/2 av dette tallet, så derfor 1/2 av det ukjente tallet X er lik 5, og hele tallet X dobbelt så mye, dvs. 5 2 = 10.

Så 5: 1 / 2 = 5 2 = 10

La oss sjekke:

La oss se på et annet eksempel. La oss si at du vil dele 6 med 2/3. La oss først prøve å finne ønsket resultat ved hjelp av tegningen (fig. 19).

Fig.19

La oss tegne et segment AB lik 6 enheter, og dele hver enhet i 3 like deler. I hver enhet er tre tredjedeler (3/3) av hele segmentet AB 6 ganger større, dvs. e. 18/3. Ved hjelp av små parentes kobler vi sammen de 18 resulterende segmentene på 2; Det vil bare være 9 segmenter. Dette betyr at brøken 2/3 er inneholdt i 6 enheter 9 ganger, eller med andre ord, brøken 2/3 er 9 ganger mindre enn 6 hele enheter. Derfor,

Hvordan få dette resultatet uten en tegning ved å bruke beregninger alene? La oss resonnere slik: vi må dele 6 med 2/3, det vil si at vi må svare på spørsmålet hvor mange ganger 2/3 er inneholdt i 6. La oss først finne ut: hvor mange ganger 1/3 er inneholdt i 6? I en hel enhet er det 3 tredjedeler, og i 6 enheter er det 6 ganger mer, dvs. 18 tredjedeler; for å finne dette tallet må vi gange 6 med 3. Dette betyr at 1/3 er inneholdt i b enheter 18 ganger, og 2/3 er inneholdt i b enheter ikke 18 ganger, men halvparten så mange ganger, dvs. 18: 2 = 9 . Derfor gjorde vi følgende når vi delte 6 med 2/3:

Herfra får vi regelen for å dele et helt tall med en brøk. For å dele et helt tall med en brøk, må du multiplisere hele tallet med nevneren til den gitte brøken, og for å gjøre dette produktet til telleren, dele det med telleren til den gitte brøken.

La oss skrive regelen med bokstaver:

For å gjøre denne regelen helt klar, bør det huskes at en brøk kan betraktes som en kvotient. Derfor er det nyttig å sammenligne den funnet regelen med regelen for å dele et tall med en kvotient, som ble angitt i § 38. Vær oppmerksom på at den samme formelen ble oppnådd der.

Ved deling er forkortelser mulige, for eksempel:

4. Å dele en brøk på en brøk.

La oss si at vi må dele 3/4 på 3/8. Hva vil tallet som resulterer fra divisjon bety? Det vil svare på spørsmålet hvor mange ganger brøken 3/8 er inneholdt i brøken 3/4. For å forstå dette problemet, la oss lage en tegning (fig. 20).

La oss ta et segment AB, ta det som ett, dele det i 4 like deler og merke 3 slike deler. Segment AC vil være lik 3/4 av segment AB. La oss nå dele hvert av de fire opprinnelige segmentene i to, så vil segmentet AB deles i 8 like deler og hver slik del vil være lik 1/8 av segmentet AB. La oss koble 3 slike segmenter med buer, da vil hvert av segmentene AD og DC være lik 3/8 av segmentet AB. Tegningen viser at et segment lik 3/8 er inneholdt i et segment lik 3/4 nøyaktig 2 ganger; Dette betyr at resultatet av divisjon kan skrives som følger:

3 / 4: 3 / 8 = 2

La oss se på et annet eksempel. La oss si at vi må dele 15/16 med 3/32:

Vi kan resonnere slik: vi må finne et tall som, etter å ha multiplisert med 3/32, vil gi et produkt lik 15/16. La oss skrive beregningene slik:

15 / 16: 3 / 32 = X

3 / 32 X = 15 / 16

3/32 ukjent nummer X er 15/16

1/32 av et ukjent antall X er ,

32 / 32 tall X sminke .

Derfor,

For å dele en brøk med en brøk, må du multiplisere telleren til den første brøken med nevneren til den andre, og multiplisere nevneren til den første brøken med telleren til den andre, og gjøre det første produktet til telleren, og den andre nevneren.

La oss skrive regelen med bokstaver:

Ved deling er forkortelser mulige, for eksempel:

5. Deling av blandede tall.

Ved deling av blandede tall må de først konverteres til uekte brøker og del deretter de resulterende brøkene i henhold til reglene for deling av brøktall. La oss se på et eksempel:

La oss konvertere blandede tall til uekte brøker:

La oss nå dele:

Derfor, for å dele blandede tall, må du konvertere dem til uekte brøker og deretter dele ved å bruke regelen for å dele brøker.

6. Finne et tall fra den gitte brøken.

Blant de forskjellige brøkproblemene er det noen ganger de der verdien av en brøkdel av et ukjent tall er gitt, og du må finne dette tallet. Denne typen problemer vil være det motsatte av problemet med å finne brøkdelen av et gitt tall; der ble det gitt et tall og det var påkrevd å finne en brøkdel av dette tallet, her ble det gitt en brøkdel av et tall og det ble påkrevd å finne dette tallet selv. Denne ideen vil bli enda tydeligere hvis vi går over til å løse denne typen problemer.

Oppgave 1. Den første dagen glaserte glassmestrene 50 vinduer, som er 1/3 av alle vinduene i det bygde huset. Hvor mange vinduer er det i dette huset?

Løsning. Problemstillingen sier at 50 glassvinduer utgjør 1/3 av alle vinduene i huset, noe som betyr at det er 3 ganger flere vinduer totalt, dvs.

Huset hadde 150 vinduer.

Oppgave 2. Butikken solgte 1500 kg mel, som er 3/8 av det totale mellageret butikken hadde. Hva var butikkens opprinnelige tilførsel av mel?

Løsning. Fra forholdene i problemet er det klart at 1500 kg solgt mel utgjør 3/8 av det totale lageret; Dette betyr at 1/8 av denne reserven vil være 3 ganger mindre, dvs. for å beregne den må du redusere 1500 med 3 ganger:

1.500:3 = 500 (dette er 1/8 av reserven).

Helt klart vil hele tilbudet være 8 ganger større. Derfor,

500 8 = 4000 (kg).

Opprinnelig lager av mel i butikken var 4000 kg.

Fra vurdering av dette problemet kan følgende regel utledes.

For å finne et tall fra en gitt verdi av brøken, er det nok å dele denne verdien med telleren til brøken og multiplisere resultatet med nevneren til brøken.

Vi løste to problemer ved å finne et tall gitt brøken. Slike problemer, som er spesielt tydelig fra den siste, løses ved to handlinger: divisjon (når en del er funnet) og multiplikasjon (når hele tallet er funnet).

Men etter at vi har lært deling av brøker, kan oppgavene ovenfor løses med én handling, nemlig: divisjon med brøk.

For eksempel kan den siste oppgaven løses i en handling som dette:

I fremtiden vil vi løse problemer med å finne et tall fra brøken med én handling - divisjon.

7. Finne et tall etter prosentandelen.

I disse problemene må du finne et tall som kjenner noen få prosent av det tallet.

Oppgave 1. I begynnelsen av dette året mottok jeg 60 rubler fra sparebanken. inntekt fra beløpet jeg la inn i sparing for ett år siden. Hvor mye penger har jeg lagt i sparebanken? (Kassene gir innskytere 2 % avkastning per år.)

Poenget med problemet er at jeg la en viss sum penger i en sparebank og ble der i ett år. Etter et år mottok jeg 60 rubler fra henne. inntekt, som er 2/100 av pengene jeg satt inn. Hvor mye penger la jeg inn?

Følgelig, når vi kjenner en del av disse pengene, uttrykt på to måter (i rubler og brøker), må vi finne hele, foreløpig ukjente, beløp. Dette er et vanlig problem med å finne et tall gitt brøken. Følgende problemer løses ved deling:

Dette betyr at 3000 rubler ble satt inn i sparebanken.

Oppgave 2. Fiskerne oppfylte månedsplanen med 64 % på to uker, og høstet 512 tonn fisk. Hva var planen deres?

Fra forholdene til problemet er det kjent at fiskerne fullførte en del av planen. Denne delen er lik 512 tonn, som er 64 % av planen. Vi vet ikke hvor mange tonn fisk som må tilberedes i henhold til planen. Å finne dette nummeret vil være løsningen på problemet.

Slike problemer løses ved divisjon:

Det betyr at det etter planen skal tilberedes 800 tonn fisk.

Oppgave 3. Toget gikk fra Riga til Moskva. Da han passerte den 276. kilometeren spurte en av passasjerene en forbipasserende konduktør hvor mye av reisen de allerede hadde tilbakelagt. Til dette svarte konduktøren: "Vi har allerede dekket 30 % av hele reisen." Hva er avstanden fra Moskva til Riga?

Fra problemforholdene er det klart at 30 % av ruten fra Riga til Moskva er 276 km. Vi må finne hele avstanden mellom disse byene, dvs. for denne delen, finne helheten:

§ 91. Gjensidige tall. Erstatte divisjon med multiplikasjon.

La oss ta brøken 2/3 og erstatte telleren i stedet for nevneren, vi får 3/2. Vi har det motsatte av denne brøken.

For å få inversen til en gitt brøk, må du sette telleren i stedet for nevneren, og nevneren i stedet for telleren. På denne måten kan vi få gjensidigheten til enhver brøk. For eksempel:

3/4, revers 4/3; 5/6, omvendt 6/5

To brøker som har egenskapen at telleren til den første er nevneren til den andre, og nevneren til den første er telleren til den andre, kalles gjensidig omvendt.

La oss nå tenke på hvilken brøk som vil være den gjensidige av 1/2. Åpenbart vil det være 2/1, eller bare 2. Ved å se etter den inverse brøkdelen av den gitte, fikk vi et heltall. Og denne saken er ikke isolert; tvert imot, for alle brøker med en teller på 1 (en), vil de gjensidige være heltall, for eksempel:

1/3, revers 3; 1/5, omvendt 5

Siden vi ved å finne gjensidige brøker også møtte heltall, vil vi i det følgende ikke snakke om gjensidige brøker, men om gjensidige tall.

La oss finne ut hvordan du skriver det inverse av et heltall. For brøker kan dette løses enkelt: du må sette nevneren i stedet for telleren. På samme måte kan du få den inverse av et heltall, siden et hvilket som helst heltall kan ha en nevner på 1. Dette betyr at inversen av 7 vil være 1/7, fordi 7 = 7/1; for tallet 10 vil inversen være 1/10, siden 10 = 10/1

Denne ideen kan uttrykkes annerledes: gjensidigheten til et gitt tall oppnås ved å dele en på et gitt tall. Denne påstanden gjelder ikke bare for hele tall, men også for brøker. Faktisk, hvis vi trenger å skrive inversen av brøken 5/9, kan vi ta 1 og dele den på 5/9, dvs.

La oss nå påpeke én ting eiendom gjensidige tall, som vil være nyttige for oss: produktet av gjensidige tall er lik én. Faktisk:

Ved å bruke denne egenskapen kan vi finne gjensidige tall på følgende måte. La oss si at vi må finne inversen til 8.

La oss betegne det med bokstaven X , deretter 8 X = 1, derfor X = 1/8. La oss finne et annet tall som er inversen av 7/12 og angi det med bokstaven X , deretter 7/12 X = 1, derfor X = 1: 7 / 12 eller X = 12 / 7 .

Vi introduserte her konseptet med gjensidige tall for litt å supplere informasjonen om å dele brøker.

Når vi deler tallet 6 med 3/5, gjør vi følgende:

Vær spesielt oppmerksom på uttrykket og sammenlign det med det gitte: .

Hvis vi tar uttrykket separat, uten sammenheng med det forrige, er det umulig å løse spørsmålet om hvor det kom fra: fra å dele 6 med 3/5 eller fra å multiplisere 6 med 5/3. I begge tilfeller skjer det samme. Derfor kan vi si at å dele ett tall med et annet kan erstattes ved å multiplisere utbyttet med inversen av divisor.

Eksemplene vi gir nedenfor bekrefter denne konklusjonen fullt ut.

) og nevner for nevner (vi får nevneren til produktet).

Formel for å multiplisere brøker:

For eksempel:

Før du begynner å multiplisere tellere og nevnere, må du sjekke om brøken kan reduseres. Hvis du kan redusere brøken, vil det være lettere for deg å gjøre ytterligere beregninger.

Å dele en vanlig brøk med en brøk.

Å dele brøker som involverer naturlige tall.

Det er ikke så skummelt som det virker. Som ved addisjon konverterer vi heltallet til en brøk med én i nevneren. For eksempel:

Multiplisere blandede fraksjoner.

Regler for å multiplisere brøker (blandet):

konvertere blandede fraksjoner til uekte fraksjoner;
multiplisere tellerne og nevnerne av brøker;
reduser fraksjonen;
Hvis du får en uekte brøk, så konverterer vi uekte brøk til en blandet brøk.

Merk!Å multiplisere blandet fraksjon til en annen blandet brøk, må du først konvertere dem til form av uekte brøker, og deretter multiplisere dem i henhold til regelen for å multiplisere vanlige brøker.

Den andre måten å multiplisere en brøk med et naturlig tall.

Det kan være mer praktisk å bruke den andre metoden for å multiplisere en vanlig brøk med et tall.

Merk!Å gange en brøk med naturlig tall Det er nødvendig å dele nevneren til brøken med dette tallet, og la telleren være uendret.

Fra eksemplet gitt ovenfor er det klart at dette alternativet er mer praktisk å bruke når nevneren til en brøk deles uten en rest med et naturlig tall.

Fleretasjes brøker.

På videregående støter man ofte på tre-etasjers (eller flere) brøker. Eksempel:

For å bringe en slik brøk til sin vanlige form, bruk divisjon gjennom 2 poeng:

Merk! Ved deling av brøker er rekkefølgen på delingen svært viktig. Vær forsiktig, det er lett å bli forvirret her.

Merk, For eksempel:

Når du deler en med en hvilken som helst brøk, vil resultatet være den samme brøken, bare invertert:

Praktiske tips for å multiplisere og dele brøker:

1. Det viktigste når du arbeider med brøkuttrykk er nøyaktighet og oppmerksomhet. Gjør alle beregninger nøye og nøyaktig, konsentrert og tydelig. Det er bedre å skrive noen ekstra linjer i utkastet enn å gå seg vill i hodeberegninger.

2. I oppgaver med forskjellige typer brøker - gå til formen for vanlige brøker.

3. Vi reduserer alle brøker til det ikke lenger er mulig å redusere.

4. Vi transformerer brøkuttrykk på flere nivåer til vanlige ved å bruke divisjon gjennom 2 punkter.

5. Del en enhet med en brøk i hodet, bare snu brøken.

La oss fortsette å studere operasjoner med vanlige brøker. Nå i søkelyset multiplisere vanlige brøker. I denne artikkelen vil vi gi en regel for å multiplisere vanlige brøker og vurdere bruken av denne regelen når vi løser eksempler. Vi vil også fokusere på å multiplisere en vanlig brøk med et naturlig tall. Avslutningsvis, la oss se på hvordan du multipliserer tre og mer brøker.

Sidenavigering.

Multiplisere en vanlig brøk med en vanlig brøk

La oss starte med ordlyden regler for å multiplisere vanlige brøker: Å multiplisere en brøk med en brøk gir en brøk hvis teller er lik produktet av tellerne til brøkene som multipliseres, og nevneren er lik produktet av nevnerne.

Det vil si at formelen tilsvarer multiplikasjonen av vanlige brøker a/b og c/d.

La oss gi et eksempel som illustrerer regelen for å multiplisere vanlige brøker. Tenk på en firkant med side 1 enhet. , mens området er 1 enhet 2. Del denne firkanten i like rektangler med sider på 1/4 enheter. og 1/8 enheter. , mens det opprinnelige kvadratet vil bestå av 4·8=32 rektangler, er derfor arealet til hvert rektangel 1/32 av arealet til det opprinnelige kvadratet, det vil si at det er lik 1/32 enheter 2 . La oss nå male over en del av den originale firkanten. Alle våre handlinger gjenspeiles i figuren nedenfor.

Sidene av det skraverte rektangelet er 5/8 enheter. og 3/4 enheter. , som betyr at arealet er lik produktet av brøkene 5/8 og 3/4, det vil si enheter 2. Men det skyggelagte rektangelet består av 15 "små" rektangler, noe som betyr at arealet er 15/32 enheter 2. Derfor,. Siden 5·3=15 og 8·4=32, kan den siste likheten skrives om som , som bekrefter formelen for å multiplisere vanlige brøker av formen .

Merk at ved å bruke den oppgitte multiplikasjonsregelen kan du multiplisere både egen- og uekte brøker, og brøker med samme nevnere, og brøker med forskjellige nevnere.

La oss vurdere eksempler på å multiplisere vanlige brøker.

Multipliser fellesbrøken 7/11 med vanlig brøk 9/8 .

Produktet av tellerne til de multipliserte brøkene 7 og 9 er lik 63, og produktet av nevnerne til 11 og 8 er lik 88. Å multiplisere de vanlige brøkene 7/11 og 9/8 gir således brøken 63/88.

Her er en kort oppsummering av løsningen: .

Vi bør ikke glemme å redusere den resulterende brøken hvis multiplikasjonen resulterer i en reduserbar brøk, og om å skille hele delen fra en uekte brøk.

Multipliser brøk 4/15 og 55/6.

La oss bruke regelen for å multiplisere vanlige brøker: .

Åpenbart er den resulterende brøken reduserbar (testen av delbarhet med 10 lar oss si at telleren og nevneren til brøken 220/90 har felles multiplikator 10). La oss redusere brøken 220/90: gcd(220, 90)=10 og . Det gjenstår å isolere hele delen fra den resulterende upassende fraksjonen: .

Merk at reduksjonen av en brøk kan utføres før du beregner produktene til tellerne og produktene av nevnerne til de multipliserte brøkene, det vil si når brøken har formen . For å gjøre dette erstattes tallene a, b, c og d av deres utvidelser til primære faktorer, hvoretter de samme faktorene til telleren og nevneren reduseres.

For avklaring, la oss gå tilbake til forrige eksempel.

Regn ut produktet av fraksjoner av formen.

I henhold til formelen for å multiplisere vanlige brøker har vi .

Siden 4=2·2, 55=5·11, 15=3·5 og 6=2·3, så . Nå reduserer vi vanlige primfaktorer: .

Alt som gjenstår er å beregne produktene i telleren og nevneren, og deretter isolere hele delen fra den uekte brøken: .

Det skal bemerkes at multiplikasjonen av brøker er preget av en kommutativ egenskap, det vil si at de multipliserte brøkene kan byttes: .

Multiplisere en vanlig brøk med et naturlig tall

La oss starte med ordlyden regler for å multiplisere en vanlig brøk med et naturlig tall: Å multiplisere en brøk med et naturlig tall gir en brøk hvis teller er lik produktet av telleren til brøken som multipliseres med det naturlige tallet, og nevneren er lik nevneren til brøken som multipliseres.

Ved å bruke bokstaver har regelen for å multiplisere en brøk a/b med et naturlig tall n formen .

Formelen følger av formelen for å multiplisere to vanlige brøker av formen. Faktisk, ved å representere et naturlig tall som en brøk med nevneren 1, får vi .

La oss se på eksempler på å multiplisere en brøk med et naturlig tall.

Multipliser brøken 2/27 med 5.

Å multiplisere telleren 2 med tallet 5 gir 10, derfor, i kraft av regelen for å multiplisere en brøk med et naturlig tall, er produktet av 2/27 med 5 lik brøken 10/27.

Det er praktisk å skrive hele løsningen slik: .

Når du multipliserer en brøk med et naturlig tall, må den resulterende brøken ofte reduseres, og hvis den også er feil, representeres den som et blandet tall.

Multipliser brøken 5/12 med tallet 8.

I følge formelen for å multiplisere en brøk med et naturlig tall, har vi . Åpenbart er den resulterende brøken reduserbar (tegnet på delbarhet med 2 indikerer felles divisor 2 for telleren og nevneren). La oss redusere brøken 40/12: siden LCM(40, 12)=4, så . Det gjenstår å fremheve hele delen: .

Her er hele løsningen: .

Legg merke til at reduksjonen kan utføres ved å erstatte tallene i telleren og nevneren med deres dekomponering til primfaktorer. I dette tilfellet vil løsningen se slik ut: .

Som konklusjon av dette punktet merker vi at å multiplisere en brøk med et naturlig tall har en kommutativ egenskap, det vil si at produktet av en brøk med et naturlig tall er lik produktet av dette naturlige tallet med brøken: .

Multiplisere tre eller flere brøker

Måten vi definerte vanlige brøker og operasjonen av multiplikasjon med dem gjør at vi kan hevde at alle egenskapene til å multiplisere naturlige tall også gjelder for å multiplisere brøker.

De kommutative og assosiative egenskapene til multiplikasjon gjør det mulig å entydig bestemme multiplisere tre eller flere brøker og naturlige tall. I dette tilfellet skjer alt analogt med multiplikasjonen av tre eller flere naturlige tall. Spesielt kan brøker og naturlige tall i et produkt omorganiseres for å lette beregningen, og i fravær av parenteser som indikerer rekkefølgen handlingene utføres i, kan vi ordne parentesene selv på en av de akseptable måtene.

La oss se på eksempler på å multiplisere flere brøker og naturlige tall.

Multipliser tre vanlige brøker 1/20, 12/5, 3/7 og 5/8.

La oss skrive ned produktet vi skal beregne . I kraft av regelen for å multiplisere brøker, er det skrevne produktet lik en brøk hvis teller er lik produktet av tellerne av alle brøker, og nevneren er lik produktet av nevnerne: .

Før du beregner produktene i telleren og nevneren, er det lurt å erstatte alle faktorene med deres dekomponering til enkle faktorer og utføre en reduksjon (du kan selvfølgelig redusere en brøk etter multiplikasjon, men i mange tilfeller krever dette mye beregningsinnsats): .

Multipliser fem tall .

I dette produktet er det praktisk å gruppere brøken 7/8 med tallet 8, og tallet 12 med brøken 5/36, dette vil forenkle beregningene, siden med en slik gruppering er reduksjonen åpenbar. Vi har
.

Multiplisere brøker

Vi vil vurdere multiplikasjonen av vanlige brøker i flere mulige alternativer.

Multiplisere en vanlig brøk med en brøk

Dette er det enkleste tilfellet der du må bruke følgende regler for multiplikasjon av brøker.

Til multipliser brøk for brøk, nødvendig:

multipliser telleren til den første brøken med telleren til den andre brøken og skriv produktet deres inn i telleren til den nye brøken;
multipliser nevneren til den første brøken med nevneren til den andre brøken og skriv produktet inn i nevneren til den nye brøken;

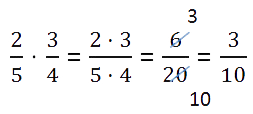
Før du multipliserer tellere og nevnere, sjekk om brøkene kan reduseres. Å redusere brøker i beregninger vil gjøre beregningene dine mye enklere.

Multiplisere en brøk med et naturlig tall

For å lage en brøk gange med et naturlig tall Du må gange telleren til brøken med dette tallet, og la nevneren for brøken være uendret.

Hvis resultatet av multiplikasjon er en uekte brøk, ikke glem å gjøre det om til et blandet tall, det vil si uthev hele delen.

Multiplisere blandede tall

For å multiplisere blandede tall, må du først gjøre dem om til uekte brøker og deretter multiplisere i henhold til regelen for å multiplisere vanlige brøker.

En annen måte å multiplisere en brøk med et naturlig tall

Noen ganger når du gjør beregninger, er det mer praktisk å bruke en annen metode for å multiplisere en vanlig brøk med et tall.

For å multiplisere en brøk med et naturlig tall, må du dele nevneren til brøken på dette tallet, og la telleren være den samme.

Som man kan se fra eksempelet, er denne versjonen av regelen mer praktisk å bruke hvis nevneren til brøken er delelig med et naturlig tall uten en rest.

Multiplisere blandede tall: regler, eksempler, løsninger.

I denne artikkelen skal vi se på multiplisere blandede tall. Først vil vi skissere regelen for å multiplisere blandede tall og vurdere bruken av denne regelen når vi løser eksempler. Deretter skal vi snakke om å multiplisere et blandet tall og et naturlig tall. Til slutt skal vi lære å multiplisere et blandet tall og en vanlig brøk.

Sidenavigering.

Multiplisere blandede tall.

Multiplisere blandede tall kan reduseres til å multiplisere vanlige brøker. For å gjøre dette er det nok å konvertere blandede tall til uekte brøker.

La oss skrive det ned multiplikasjonsregel for blandet tall:

Først må de blandede tallene som multipliseres erstattes med uekte brøker;
For det andre må du bruke regelen for å multiplisere brøker med brøker.

La oss se på eksempler på bruk av denne regelen når du multipliserer et blandet tall med et blandet tall.

Utfør multiplikasjon av blandede tall og .

Først, la oss representere de blandede tallene som multipliseres som uekte brøker: Og . Nå kan vi erstatte multiplikasjonen av blandede tall med multiplikasjonen av vanlige brøker: . Ved å bruke regelen for å multiplisere brøker får vi . Den resulterende brøken er irreduserbar (se reduserbare og irreduserbare brøker), men den er upassende (se riktige og uekte brøker), derfor gjenstår det for å få det endelige svaret å isolere hele delen fra den uekte brøken: .

La oss skrive hele løsningen på én linje: .

For å styrke ferdighetene med å multiplisere blandede tall, vurder å løse et annet eksempel.

Utfør multiplikasjon.

Morsomme tall og er lik henholdsvis brøkene 13/5 og 10/9. Deretter . På dette stadiet er det på tide å huske på å redusere en brøk: Erstatt alle tallene i brøken med deres nedbrytninger til primfaktorer, og utfør en reduksjon av identiske faktorer.

Multiplisere et blandet tall og et naturlig tall

Etter å ha erstattet et blandet tall med en uekte brøk, multiplisere et blandet tall og et naturlig tall fører til multiplikasjon av en vanlig brøk og et naturlig tall.

Multipliser et blandet tall og det naturlige tallet 45.

Et blandet tall er lik en brøk, da . La oss erstatte tallene i den resulterende brøken med deres dekomponering til primfaktorer, utføre en reduksjon og deretter velge hele delen: .

Multiplikasjon av et blandet tall og et naturlig tall utføres noen ganger praktisk ved å bruke den distributive egenskapen til multiplikasjon i forhold til addisjon. I dette tilfellet er produktet av et blandet tall og et naturlig tall lik summen av produktene til heltallsdelen med det gitte naturlige tallet og brøkdelen med det gitte naturlige tallet, det vil si, .

Beregn produktet.

La oss erstatte det blandede tallet med summen av heltalls- og brøkdelene, hvoretter vi bruker den fordelende egenskapen til multiplikasjon: .

Multiplisere blandede tall og brøker Det er mest praktisk å redusere det til multiplikasjonen av vanlige brøker ved å representere det blandede tallet som multipliseres som en uekte brøk.

Multipliser det blandede tallet med fellesbrøken 4/15.

Å erstatte det blandede tallet med en brøk, får vi .

Multiplisere brøker

§ 140. Definisjoner. 1) Å multiplisere en brøk med et heltall er definert på samme måte som å multiplisere heltall, nemlig: å multiplisere et tall (multiplikand) med et heltall (faktor) betyr å komponere en sum av identiske ledd, der hvert ledd er lik multiplikanden, og antall ledd er lik multiplikatoren.

Så å multiplisere med 5 betyr å finne summen:
2) Å multiplisere et tall (multiplikand) med en brøk (faktor) betyr å finne denne brøkdelen av multiplikanden.

Derfor vil vi nå kalle å finne en brøkdel av et gitt tall, som vi vurderte før, multiplikasjon med en brøk.

3) Å multiplisere et tall (multiplikand) med et blandet tall (faktor) betyr å multiplisere multiplikasjonen først med hele tallet til multiplikatoren, deretter med brøkdelen av multiplikatoren, og legge sammen resultatene av disse to multiplikasjonene.

For eksempel:

Tallet oppnådd etter multiplikasjon i alle disse tilfellene kalles arbeid, dvs. det samme som når man multipliserer heltall.

Fra disse definisjonene er det klart at multiplikasjon av brøktall er en handling som alltid er mulig og alltid entydig.

§ 141. Hensiktsmessigheten av disse definisjonene. For å forstå det tilrådelige med å introdusere de to siste definisjonene av multiplikasjon i aritmetikk, la oss ta følgende problem:

Oppgave. Et tog, som beveger seg jevnt, dekker 40 km i timen; hvordan finne ut hvor mange kilometer dette toget vil reise i løpet av et gitt antall timer?

Hvis vi forble med den ene definisjonen av multiplikasjon, som er indikert i heltallsaritmetikk (tillegg av like ledd), så ville problemet vårt ha tre ulike løsninger, nemlig:

Hvis det gitte antallet timer er et heltall (for eksempel 5 timer), må du multiplisere 40 km med dette antallet timer for å løse problemet.

Hvis et gitt antall timer uttrykkes som en brøk (for eksempel en time), må du finne verdien av denne brøken fra 40 km.

Til slutt, hvis det gitte antallet timer er blandet (for eksempel timer), må 40 km multipliseres med heltallet i det blandede tallet, og til resultatet legge til en annen brøkdel av 40 km, som er i det blandede tallet. Antall.

Definisjonene vi har gitt tillater oss å gi ett generelt svar på alle disse mulige tilfellene:

du må gange 40 km med et gitt antall timer, uansett hva det måtte være.

Derfor, hvis problemet presenteres i generell form som følger:

Et tog som beveger seg jevnt, dekker v km på en time. Hvor mange kilometer vil toget kjøre på t timer?

så, uansett hva tallene v og t er, kan vi gi ett svar: det ønskede tallet uttrykkes med formelen v · t.

Merk. Å finne en brøkdel av et gitt tall, etter vår definisjon, betyr det samme som å multiplisere et gitt tall med denne brøken; derfor, for eksempel, å finne 5 % (dvs. fem hundredeler) av et gitt tall betyr det samme som å multiplisere et gitt tall med eller med ; å finne 125 % av et gitt tall betyr det samme som å multiplisere dette tallet med eller med osv.

§ 142. En merknad om når et tall øker og når det avtar fra multiplikasjon.

Multiplikasjon med en egenbrøk reduserer tallet, og multiplikasjon med en uekte brøk øker tallet hvis denne uekte brøken mer enn en, og forblir uendret hvis den er lik én.
Kommentar. Når du multipliserer brøktall, så vel som heltall, tas produktet lik null hvis noen av faktorene er lik null, så .

§ 143. Utledning av multiplikasjonsregler.

1) Multiplisere en brøk med et helt tall. La en brøk ganges med 5. Dette betyr økt med 5 ganger. For å øke en brøk med 5 ganger, er det nok å øke telleren eller redusere nevneren med 5 ganger (§ 127).

Derfor:
Regel 1. For å multiplisere en brøk med et helt tall, må du multiplisere telleren med dette hele tallet, men la nevneren være den samme; i stedet kan du også dele nevneren til brøken med det gitte hele tallet (hvis mulig), og la telleren være den samme.

Kommentar. Produktet av en brøk og dens nevner er lik telleren.

Så:
Regel 2. For å multiplisere et helt tall med en brøk, må du multiplisere hele tallet med telleren til brøken og gjøre dette produktet til telleren, og signere nevneren til denne brøken som nevneren.
Regel 3. For å multiplisere en brøk med en brøk, må du multiplisere telleren med telleren og nevneren med nevneren, og gjøre det første produktet til telleren, og det andre til produktets nevner.

Kommentar. Denne regelen kan også brukes til å multiplisere en brøk med et heltall og et heltall med en brøk, hvis vi bare ser på heltallet som en brøk med nevneren en. Så:

Dermed er de tre reglene som nå er skissert inne i én, som generelt kan uttrykkes som følger:
4) Multiplikasjon av blandede tall.

Regel 4. For å multiplisere blandede tall, må du konvertere dem til uekte brøker og deretter multiplisere i henhold til reglene for å multiplisere brøker. For eksempel:
§ 144. Reduksjon ved multiplikasjon. Når du multipliserer brøker, om mulig, er det nødvendig å foreta en foreløpig reduksjon, som kan sees av følgende eksempler:

En slik reduksjon kan gjøres fordi verdien av en brøk ikke vil endres hvis dens teller og nevner reduseres med samme antall ganger.

§ 145. Endring av et produkt med skiftende faktorer. Når faktorene endres, vil produktet av brøktall endre seg på nøyaktig samme måte som produktet av heltall (§ 53), nemlig: hvis du øker (eller reduserer) en faktor flere ganger, så vil produktet øke (eller reduseres) med samme beløp.

Så hvis i eksemplet:
for å multiplisere flere brøker, må du multiplisere deres tellere med hverandre og nevnerne med hverandre og gjøre det første produktet til telleren, og det andre til produktets nevner.

Kommentar. Denne regelen kan også brukes på slike produkter der noen av faktorene til tallet er heltall eller blandet, hvis bare vi ser på heltallet som en brøk med en nevner på én, og vi gjør blandede tall om til uekte brøker. For eksempel:
§ 147. Grunnleggende egenskaper ved multiplikasjon. De egenskapene til multiplikasjon som vi indikerte for heltall (§ 56, 57, 59) gjelder også for multiplikasjon av brøktall. La oss angi disse egenskapene.

1) Produktet endres ikke når faktorene endres.

For eksempel:

Faktisk, i henhold til regelen i forrige avsnitt, er det første produktet lik brøkdelen, og det andre er lik brøkdelen. Men disse brøkene er de samme, fordi deres vilkår er forskjellige bare i rekkefølgen av heltallsfaktorene, og produktet av heltall endres ikke når stedene til faktorene endres.

2) Produktet vil ikke endres hvis noen gruppe faktorer erstattes av deres produkt.

For eksempel:

Resultatene er de samme.

Fra denne egenskapen til multiplikasjon kan følgende konklusjon trekkes:

for å multiplisere et tall med et produkt, kan du multiplisere dette tallet med den første faktoren, multiplisere det resulterende tallet med det andre osv.

For eksempel:
3) Distributiv lov om multiplikasjon (i forhold til addisjon). For å multiplisere en sum med et tall, kan du multiplisere hvert ledd separat med det tallet og legge til resultatene.

Denne loven ble forklart av oss (§ 59) som brukt på heltall. Det forblir sant uten endringer for brøktall.

La oss vise, faktisk, at likheten

(a + b + c + .)m = am + bm + cm + .

(den distributive loven om multiplikasjon i forhold til addisjon) forblir sann selv når bokstavene betyr brøktall. La oss vurdere tre tilfeller.

1) La oss først anta at faktoren m er et heltall, for eksempel m = 3 (a, b, c – alle tall). I henhold til definisjonen av multiplikasjon med et heltall, kan vi skrive (begrense oss til tre termer for enkelhets skyld):

(a + b + c) * 3 = (a + b + c) + (a + b + c) + (a + b + c).

Ut fra den assosiative addisjonsloven kan vi utelate alle parentesene på høyre side; Ved å bruke den kommutative loven om addisjon, og deretter igjen den assosiative loven, kan vi åpenbart omskrive høyresiden som følger:

(a + a + a) + (b + b + b) + (c + c + c).

(a + b + c) * 3 = a * 3 + b * 3 + c * 3.

Dette betyr at fordelingsloven stadfestes i denne saken.

Å dele en brøk på et naturlig tall

Seksjoner: Matematikk

T leksjonstype: ONZ (oppdagelse av ny kunnskap - ved hjelp av teknologien til den aktivitetsbaserte undervisningsmetoden).

Utlede metoder for å dele en brøk med et naturlig tall;
Utvikle evnen til å dele en brøk på et naturlig tall;
Gjenta og forsterk deling av brøker;
Trene opp evnen til å redusere brøker, analysere og løse problemer.

Utstyr demonstrasjonsmateriale:

1. Oppgaver for å oppdatere kunnskap:

2. Prøve (individuell) oppgave.

1. Utfør deling:

2. Utfør divisjon uten å utføre hele kjeden av beregninger: .

Når du deler en brøk på et naturlig tall, kan du multiplisere nevneren med det tallet, men la telleren være den samme.

Hvis telleren er delelig med et naturlig tall, kan du dele telleren på tallet når du deler en brøk med dette tallet og la nevneren være den samme.

I. Motivasjon (selvbestemmelse) for pedagogisk virksomhet.

Organisere oppdatering av krav til studenten når det gjelder utdanningsaktiviteter ("must");
Organisere studentaktiviteter for å etablere tematiske rammer ("Jeg kan");
Skape forutsetninger for at eleven kan utvikle et internt behov for inkludering i pedagogiske aktiviteter («Jeg vil»).

Organisering av utdanningsprosessen på stadium I.

Hallo! Jeg er glad for å se dere alle på mattetimen. Jeg håper det er gjensidig.

Gutter, hvilken ny kunnskap tilegnet dere i forrige leksjon? (Del brøker).

Ikke sant. Hva hjelper deg med å dele brøker? (Regel, egenskaper).

Hvor trenger vi denne kunnskapen? (I eksempler, ligninger, problemer).

Bra gjort! Du gjorde det bra på oppgavene i forrige leksjon. Vil du oppdage ny kunnskap selv i dag? (Ja).

Så - la oss gå! Og mottoet for leksjonen vil være utsagnet "Du kan ikke lære matematikk ved å se på naboen din gjøre det!"

II. Oppdatere kunnskap og fikse individuelle vansker i en prøvehandling.

Organisere oppdatering av lærte handlingsmetoder tilstrekkelig til å bygge ny kunnskap. Registrer disse metodene verbalt (i tale) og symbolsk (standard) og generaliser dem;
Organiser oppdatering mentale operasjoner og kognitive prosesser tilstrekkelig til å konstruere ny kunnskap;
Motivere for en prøvehandling og dens uavhengige gjennomføring og begrunnelse;
Tilstede individuell oppgave for en prøvehandling og analysere den for å identifisere nytt pedagogisk innhold;
Organiser fiksering av det pedagogiske målet og emnet for leksjonen;
Organiser gjennomføringen av en prøvehandling og fiks problemet;
Organiser en analyse av de mottatte svarene og noter individuelle vanskeligheter med å utføre en prøvehandling eller rettferdiggjøre den.

Organisering av utdanningsprosessen på trinn II.

Foran ved bruk av nettbrett (individuelle brett).

1. Sammenlign uttrykk:

(Disse uttrykkene er like)

Hvilke interessante ting la du merke til? (Telleren og nevneren for utbyttet, telleren og nevneren for divisor i hvert uttrykk økt med samme antall ganger. Dermed er utbytte og divisorer i uttrykkene representert med brøker som er like med hverandre).

Finn betydningen av uttrykket og skriv det ned på nettbrettet ditt. (2)

Hvordan kan jeg skrive dette tallet som en brøk?

Hvordan utførte du divisjonshandlingen? (Barn resiterer regelen, læreren henger den på tavlen bokstavbetegnelser)

2. Beregn og registrer kun resultatene:

3. Legg sammen resultatene og skriv ned svaret. (2)

Hva heter nummeret som ble oppnådd i oppgave 3? (Naturlig)

Tror du du kan dele en brøk på et naturlig tall? (Ja, vi prøver)

Prøv dette.

4. Individuell (prøve)oppgave.

Utfør divisjon: (kun eksempel a)

Hvilken regel brukte du for å dele? (I henhold til regelen om å dele brøker med brøker)

Del nå brøken med et naturlig tall større enn på en enkel måte, uten å utføre hele kjeden av beregninger: (eksempel b). Jeg gir deg 3 sekunder for dette.

Hvem klarte ikke å fullføre oppgaven på 3 sekunder?

Hvem gjorde det? (Det finnes ingen slike)

Hvorfor? (Vi vet ikke veien)

Hva fikk du? (Vanskelighet)

Hva tror du vi skal gjøre i klassen? (Del brøker med naturlige tall)

Det er riktig, åpne notatbøkene og skriv ned emnet for leksjonen: "Å dele en brøk med et naturlig tall."

Hvorfor høres dette emnet nytt ut når du allerede vet hvordan du deler brøker? (Trenge ny måte)

Ikke sant. I dag skal vi etablere en teknikk som forenkler delingen av en brøk med et naturlig tall.

III. Identifisere plasseringen og årsaken til problemet.

Organiser restaureringen av fullførte operasjoner og registrer (verbal og symbolsk) stedet - trinn, operasjon - hvor vanskeligheten oppsto;
Organiser korrelasjonen mellom elevenes handlinger med metoden (algoritmen) som brukes og fiksering i ekstern tale av årsaken til vanskeligheten - den spesifikke kunnskapen, ferdighetene eller evnene som mangler for å løse det første problemet av denne typen.

Organisering av utdanningsprosessen på trinn III.

Hvilken oppgave måtte du fullføre? (Del en brøk med et naturlig tall uten å gå gjennom hele kjeden av beregninger)

Hva forårsaket deg problemer? (Kunne ikke bestemme meg for en kort tid rask måte)

Hvilket mål setter vi oss selv i timen? (Finne rask måteå dele en brøk på et naturlig tall)

Hva vil hjelpe deg? (Allerede kjent regel for å dele brøker)

IV. Bygge et prosjekt for å komme ut av et problem.

Avklaring av prosjektmålet;
Valg av metode (avklaring);
Bestemmelse av middel (algoritme);
Bygge en plan for å nå målet.

Organisering av utdanningsprosessen på trinn IV.

La oss gå tilbake til testoppgaven. Du sa at du delte etter regelen for å dele brøker? (Ja)

For å gjøre dette, erstatte det naturlige tallet med en brøk? (Ja)

Hvilket trinn (eller trinn) tror du kan hoppes over?

(Løsningskjeden er åpen på tavlen:

Analyser og trekk en konklusjon. (Trinn 1)

Hvis det ikke er noe svar, så leder vi deg gjennom spørsmål:

Hvor ble det av den naturlige deleren? (Inn i nevneren)

Har telleren endret seg? (Nei)

Så hvilket trinn kan du "utelate"? (Trinn 1)

Multipliser nevneren til en brøk med et naturlig tall.
Vi endrer ikke telleren.
Vi får en ny brøkdel.

V. Gjennomføring av det konstruerte prosjektet.

Organisere kommunikativ interaksjon for å implementere det konstruerte prosjektet rettet mot å tilegne seg den manglende kunnskapen;
Organisere registreringen av den konstruerte handlingsmetoden i tale og tegn (ved hjelp av en standard);
Organiser løsningen på det første problemet og noter hvordan du kan overvinne vanskeligheten;
Organisere klargjøring av ny kunnskaps generelle natur.

Organisering av utdanningsprosessen på trinn V.

Kjør nå testsaken på en ny måte raskt.

Nå klarte du å fullføre oppgaven raskt? (Ja)

Forklar hvordan du gjorde dette? (Barn snakker)

Det betyr at vi har fått ny kunnskap: regelen for å dele en brøk på et naturlig tall.

Bra gjort! Si det i par.

Deretter snakker en elev til klassen. Vi fikser regelalgoritmen verbalt og i form av en standard på tavlen.

Skriv inn bokstavbetegnelsene og skriv ned formelen for regelen vår.

Eleven skriver på tavlen og sier regelen: når du deler en brøk på et naturlig tall, kan du multiplisere nevneren med dette tallet, men la telleren være den samme.

(Alle skriver formelen i notatbøkene sine).

Analyser nå kjeden for å løse testoppgaven igjen, og vær spesielt oppmerksom på svaret. Hva gjorde du? (Telleren til brøken 15 ble delt (redusert) med tallet 3)

Hva er dette nummeret? (Naturlig, divisor)

Så hvordan kan du ellers dele en brøk på et naturlig tall? (Sjekk av: hvis telleren til en brøk er delelig med dette naturlige tallet, så kan du dele telleren på dette tallet, skrive resultatet i telleren til den nye brøken og la nevneren være den samme)

Skriv ned denne metoden som en formel. (Eleven skriver regelen på tavlen mens han uttaler den. Alle skriver formelen i notatbøkene sine.)

La oss gå tilbake til den første metoden. Du kan bruke den hvis a:n? (Ja det generell metode)

Og når er det praktisk å bruke den andre metoden? (Når telleren til en brøk er delt på et naturlig tall uten en rest)

VI. Primær konsolidering med uttale i ytre tale.

Organiser barnas assimilering av en ny handlingsmetode når de løser standardproblemer med deres uttale i ekstern tale (frontalt, i par eller grupper).

Organisering av utdanningsprosessen på trinn VI.

Beregn på en ny måte:

nr. 363 (a; d) - utført ved styret, uttale regelen.
nr. 363 (e; f) - parvis med kontroll i henhold til prøven.

VII. Selvstendig arbeid med selvtest etter standard.

Organiser studentenes uavhengige fullføring av oppgaver for en ny måte å handle på;
Organiser selvtest basert på sammenligning med standarden;
Basert på resultatene av utførelse selvstendig arbeid organisere refleksjon over assimilering av en ny måte å handle på.

Organisering av utdanningsprosessen på trinn VII.

Beregn på en ny måte:

Elevene sjekker mot standarden og markerer riktigheten av utførelse. Årsakene til feil analyseres og feil korrigeres.

Læreren spør de elevene som gjorde feil, hva er årsaken?

På dette stadiet er det viktig at hver student selvstendig sjekker arbeidet sitt.

Før du løser oppgave 8), vurder et eksempel fra læreboken:

IX. Refleksjon over læringsaktiviteter i klasserommet.

Organiser opptak av nytt innhold lært i leksjonen;
Organisere en reflekterende analyse av pedagogiske aktiviteter fra synspunktet om å oppfylle kravene kjent for studentene;
Organisere elevenes vurdering av egne aktiviteter i timen;
Organiser registreringen av uløste vanskeligheter i leksjonen som en retning for fremtidige pedagogiske aktiviteter;
Organiser en diskusjon og opptak av lekser.

Organisering av utdanningsprosessen på trinn IX.

Gutter, hvilken ny kunnskap har dere oppdaget i dag? (Lærte å dele en brøk på et naturlig tall på en enkel måte)

Formuler en generell metode. (De sier)

På hvilken måte og i hvilke tilfeller kan du bruke det? (De sier)

Hva er fordelen med den nye metoden?

Har vi nådd leksjonsmålet? (Ja)

Hvilken kunnskap brukte du for å nå målet ditt? (De sier)

Har alt ordnet seg for deg?

Hva var vanskelighetene?

Sidenavigering.

Multiplisere blandede tall.

Multiplisere blandede tall kan reduseres til å multiplisere vanlige brøker. For å gjøre dette er det nok å konvertere blandede tall til uekte brøker.

La oss skrive det ned multiplikasjonsregel for blandet tall:

Først må de blandede tallene som multipliseres erstattes med uekte brøker;
For det andre må du bruke regelen for å multiplisere brøker med brøker.

La oss se på eksempler på bruk av denne regelen når du multipliserer et blandet tall med et blandet tall.

Utfør multiplikasjon av blandede tall og .

La oss skrive hele løsningen på én linje: .

For å styrke ferdighetene med å multiplisere blandede tall, vurder å løse et annet eksempel.

Utfør multiplikasjon.

Multiplisere et blandet tall og et naturlig tall

Etter å ha erstattet et blandet tall med en uekte brøk, multiplisere et blandet tall og et naturlig tall fører til multiplikasjon av en vanlig brøk og et naturlig tall.

Multipliser et blandet tall og det naturlige tallet 45.

Et blandet tall er lik en brøk, da . La oss erstatte tallene i den resulterende brøken med deres dekomponering til primfaktorer, utføre en reduksjon og deretter velge hele delen: .

Beregn produktet.

La oss erstatte det blandede tallet med summen av heltalls- og brøkdelene, hvoretter vi bruker den fordelende egenskapen til multiplikasjon: .

Multiplisere blandede tall og brøker Det er mest praktisk å redusere det til multiplikasjonen av vanlige brøker ved å representere det blandede tallet som multipliseres som en uekte brøk.

Multipliser det blandede tallet med fellesbrøken 4/15.

Å erstatte det blandede tallet med en brøk, får vi .

www.cleverstudents.ru

Multiplisere brøker

Så å multiplisere med 5 betyr å finne summen:
2) Å multiplisere et tall (multiplikand) med en brøk (faktor) betyr å finne denne brøkdelen av multiplikanden.

Derfor vil vi nå kalle å finne en brøkdel av et gitt tall, som vi vurderte før, multiplikasjon med en brøk.

For eksempel:

Tallet oppnådd etter multiplikasjon i alle disse tilfellene kalles arbeid, dvs. det samme som når man multipliserer heltall.

Fra disse definisjonene er det klart at multiplikasjon av brøktall er en handling som alltid er mulig og alltid entydig.

§ 141. Hensiktsmessigheten av disse definisjonene. For å forstå det tilrådelige med å introdusere de to siste definisjonene av multiplikasjon i aritmetikk, la oss ta følgende problem:

Oppgave. Et tog, som beveger seg jevnt, dekker 40 km i timen; hvordan finne ut hvor mange kilometer dette toget vil reise i løpet av et gitt antall timer?

Hvis vi forble med den ene definisjonen av multiplikasjon som er indikert i heltallsaritmetikk (tillegg av like vilkår), ville problemet vårt ha tre forskjellige løsninger, nemlig: