Complex numbers

Imaginary and complex numbers. Absolus and ordinate

integrated number. Combined complex numbers.

Operations with complex numbers. Geometric

representation of complex numbers. Complex plane.

The module and the integrated number argument. Trigonometric

the form of an integrated number. Operations with complex

Numbers in trigonometric form. Moauro formula.

Officer O. imaginary and complex numbers Led in the section "Mimic and complex numbers". The need for these numbers of the new type appeared when solving square equations for the caseD.< 0 (здесь D. - discriminant square equation). For a long time, these numbers did not find physical applies, so they were called "imaginary" numbers. However, now they are very widely used in various fields of physics.

both technology: electrical engineering, hydro and aerodynamics, theory of elasticity, etc.

Complex numbers record in the form: A + BI.. Here a.and b. – actual numbers , but i. – imaginary unit, t.e. I. 2 = –1. Number a.called abscissa, A. b - Ordate integrated numbera + Bi.Two complex numbersa + BI and a - BI. called conjugated complex numbers.

Major agreements:

1. Valid number butcan also be recorded in the form Integrated number:a +.0 i.or a -0 i.. For example, recording 5 + 0 I. and 5 - 0 i.mean the same number5 .

2. Comprehensive number 0 + bI called purely imaginary number. RecordbImeans the same as 0 + bI.

3. Two complex numbers A + BI. andc + DIare considered equal ifa \u003d C.and b \u003d D.. Otherwise Complex numbers are not equal.

Addition. Sum of complex numbersa + BI and c + DIcalled a complex number (a + C. ) + (b + D. ) i.In this way, when adding integrated numbers, their abscissas and orders are separately folded.

This definition complies with the rules of action with conventional polynomials.

Subtraction. The difference between two complex numbersa + BI (reduced) and C + DI (subtracted) called a complex number ( A - C. ) + (b - D. ) i.

In this way, when subtracting two integrated numbers, their abscissas and orders are separately submitted.

Multiplication. Product complex numbersa + BI and c + DI the integrated number is called:

( AC - BD. ) + (aD + BC. ) i.This definition follows from two requirements:

1) Numbers a + BI and c + DImust multiply as algebraic bicked

2) Number I. It has basic property:i. 2 = – 1.

PRI MERS ( a + BI )( A - BI.) \u003d A. 2 + B. 2 . Hence, composition

two conjugate integrated numbers equal to valid

positive number.

Division. Split a complex numbera + BI (divide) to another C + DI(divider) - it means to find the third numbere + F I (CHANT), which is multiplied by the dividerc + DI, as a result, divisiblea + Bi.

If the divider is not equal to zero, the division is always possible.

PRI MERS Find (8 + I. ) : (2 – 3 i.) .

R E W E N E. I rewrite this attitude in the form of a fraction:

Multiplying its numerator and denominator for 2 + 3i.

AND After performing all the transformations, we get:

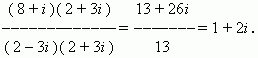
Geometric representation of complex numbers. Real numbers are depicted by dots on a numeric direct:

Here point A.means the number -3, pointB. - number 2, and O. - zero. In contrast, complex numbers are depicted by points on the coordinate plane. We choose rectangular (Cartesome) coordinates with the same scale on both axes. Then complex number A + BI. will be represented by point P with abscissa A and ordinary b (See Fig.). This coordinate system is called complex plane .

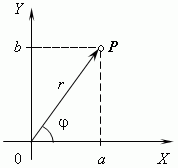
Module integrated number called vector length Op.depicting a complex number on the coordinate ( comprehensive) Plane. A complex number module A + BI. denotes | a + BI | or letter r.

Go) numbers.

2. Algebraic form of comprehensive numbers

Integrated number or complex called a number consisting of two numbers (parts) - real and imaginary.

Real It is called any positive or negative number, for example, + 5, - 28, and the like. Denote the real number of letter "L".

Imaginarythe number is called the product equal to the product of a real number into a square root from a negative unit, for example, 8, - 20, and the like.

Negative unit called imaginary And denotes the letter "Yot":

Denote the real number of the imaginary letter "M".

Then imaginary number can be written as follows: J M. In this case, a complex number can be written as follows:

A \u003d L + J M (2).

Such a form of an integrated number (complex) record, which is an algebraic amount of real and imaginary parts, is called algebraic.

Example 1. Present in algebraic form complex, the real part of which is equal to 6, and the imaginary 15.

Decision. A \u003d 6 + J 15.

In addition to algebraic, a complex number can be represented by three more:

1. graphic;

2. trigonometric;

3. Indicative.

Such a variety of forms sharply simplify calculations sinusoidal values \u200b\u200band their graphic image.

Alternately consider the graphic, trigonometric and indicator

forms of presentation of complex numbers.

Graphic form of comprehensive numbers

For the graphical representation of complex numbers apply straight

coal coordinate system. In the usual (school) coordinate system along the X axes (abscissa axis) and "Y" (the ordinate axis), positive or negative are postponed real numbers.

In the same coordinate system adopted in the symbolic method, along the X axis

in the form of segments, actual numbers are laid, and along the axis "y" - imaginary

Fig. 1. Coordinate system for graphic image of complex numbers

Therefore, the axis of the abscissa "X" is called the axis of real magnitudes or, to reduce, real axis.

The ordinate axis is called the axis of imaginary quantities or imaginary axis.

The same plane (i.e., the plane of the figure), which depicts complex numbers or values, are called comprehensive plane.

In this plane, the complex number A \u003d L + J M is shown by vector

(Fig. 2), the projection of which to the real axis is equal to its real part RE A \u003d A "\u003d L, and the projection on the imaginary axis - the imaginary part of IM A \u003d A" \u003d M.

(Real - Real - Real, Valid, Real, Im - from English.imaginary - unreal, imaginary).

Fig. 2. Graphic representation of a complex number

In this case, the number A can be written so

A \u003d A "+ A" \u003d RE A + J Im A (3).

Using a graphic image of the number A in the complex plane, we introduce new definitions and get some important relations:

1. the length of the vector is called module vector and denotes | A |.

According to Pythagora theorem

| A | \u003d. (4) .

2. Angleα formed by vector A and real positive

axis called argument vector A and is determined through his tangent:

tG α \u003d A "/ A" \u003d IM A / RE A (5).

Thus, for the graphical representation of the integrated number

A \u003d a "+ a" in the form of a vector it is necessary:

1. Find a vector module | A | by formula (4);

2. Find the argument of the TG α vector according to formula (5);

3. Find the angle α from the ratio α \u003d Arc TG α;

4. In the coordinate system J (x), at an angle α auxiliary

direct and on it on a certain scale to postpone the segment equal to the module of the vector | A |.

Example 2. The complex number A \u003d 3 + J 4 is present in graphical form.

Complex numbers I.
Coordinate
plane

The geometric model of the set R valid numbers is the numerical straight line. Any actual number corresponds to the only point

on the
numerical direct and, any point direct
only one corresponds to one
Valid number!

After adding to a numeric direct, corresponding set of all valid numbers, another dimension is a straight line containing a plurality of pure M

Adding to a numeric direct corresponding set
All valid numbers are another dimension -
Direct containing many purely imaginary numbers -
We obtain the coordinate plane in which everyone
An integrated number A + Bi can be put in line with
Point (a; b) of the coordinate plane.
i \u003d 0 + 1i corresponds to the point (0; 1)
2 + 3i corresponds to the point (2; 3)
-i-4 corresponds to the point (-4; -1)
5 \u003d 5 + 1i corresponds to longing (5; 0)

Geometric meaning of interconnection operation

! Interface operation is axial
Symmetry relative to the abscissa axis.
!! Combated friend
integrated numbers are equal to
The start of coordinates.
!!! Vector depicting
Conjugated numbers, tilted to the axis
abscissa at the same angle but
located on different sides of
of this axis.

Image of valid numbers

An image of complex numbers

Algebraic
method
Images:
Complex number
A + Bi is depicted
Point plane
With coordinates
(a; b)

Examples of the image of complex numbers on the coordinate plane

(We are interested
complex numbers
z \u003d x + yi, whose
x \u003d -4. This equation
straight,
parallel axis
ordinate)
W.
X \u003d - 4
Valid
Part equal to -4.
0
H.

Position the set of all complex numbers on the coordinate plane, which:

Imaginary part
is even
Sneblycious
Natural
Number
(We are interested
complex numbers
z \u003d x + yi, whose
y \u003d 2,4,6,8.
Geometric image
consists of four
straight, parallel
abscissa axis)
W.
8
6
4
2
0
H.

The setting of a complex number is equivalent to the task of two valid numbers A, B - the actual and imaginary parts of this integrated number. But the unlawful pair of numbers is depicted in a decartal rectangular coordinate system with coordinates Thus, this point can be an image and for a complex number Z: between complex numbers and points of the coordinate plane establishes a mutually unambiguous compliance. When using the coordinate plane for the image of the complex numbers, the OK axis is commonly called the actual axis (since the actual part of the number is taken for the abscissue of the point), and the axis of the OU-imaginary axis (since the imaginary part of the number is accepted by the order). The complex number Z, depicted by the point (A, B), is called the affix of this point. In this case, the actual numbers are depicted by dots lying on the actual axis, and all purely imaginary numbers (at a \u003d 0) - dots lying on the imaginary axis. The number of zero is depicted by the point O.

In fig. 8 Built images of numbers.

Two complex conjugate numbers are depicted by points, symmetrical with respect to the axis oh (points in Fig. 8).

Often with a complex number are associated not only by the point M, depicting this number, but also the vector Ohms (see paragraph 93), which is leading from about in m; An image of a number of vector is convenient from the point of view of geometric interpretation of the accumulation and subtraction of complex numbers.

In fig. 9, and it is shown that the vector depicting the amount of complex numbers is obtained as a diagonal of the parallelogram, built in the vector images of the components.

This rule of the formation of vectors is known as a rule parallelogram (for example, for the addition of forces or speeds in the course of physics). Subtraction can be reduced to the opposite vector (Fig. 9, b).

As is known (paragraph 8), the position of the point on the plane can also be set in its polar coordinates. Therefore, the complex number - the affix point is also determined by the task from fig. 10 It is clear that at the same time the integrated number module: the polar radius of the point depicting the number is equal to the module of this number.

The polar angle of the point M is called the argument of the number depicted by this point. The integrated number argument (as well as the polar angle of the point) is determined ambiguously; If - one of its values, then all its values \u200b\u200bare expressed by the formula

All values \u200b\u200bof the argument in the aggregate are denoted by the symbol.

So, any complex number can be put in compliance with a pair of valid numbers: the module and the argument of this number, and the argument is determined ambiguously. On the contrary, the specified module and argument corresponds to a single number that has data module and argument. Special properties have the number of zero: its module is zero, the argument does not attribute any definite value.

To achieve unambiguity in determining the argument of a complex number, one of the values \u200b\u200bof the argument can be called the main thing. It is denoted by a symbol. Usually, the value satisfying inequalities is selected as the main value of the argument.

(in other cases inequalities).

We still pay attention to the values \u200b\u200bof the argument of valid and purely imaginary numbers:

The actual and imaginary parts of the integrated number (as the Cartesian coordinate points) are expressed through its module and the argument (polar coordinates of the point) using formulas (8.3):

and the complex number can be recorded in the following trigonometric form.