Лекции по теоретична механика
Точкова динамика
Лекция 1
Основни понятия за динамиката
В гл Динамикаизучава се движението на телата под действието на приложените към тях сили. Следователно, в допълнение към понятията, които бяха въведени в раздела кинематика,тук е необходимо да се използват нови понятия, които отразяват спецификата на въздействието на силите върху различни тела и реакцията на телата на тези влияния. Нека разгледаме основните от тези понятия.
а) сила
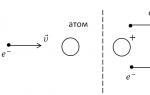
Силата е количествен резултат от въздействието върху дадено тяло от други тела.Силата е векторна величина (фиг. 1).
![]()
![]()
Точка А от началото на вектора на силата ФНаречен точка на приложение на силата... Нарича се правата MN, на която е разположен векторът на силата линия на действие на сила.Дължината на вектора на силата, измерена в определен мащаб, се нарича числова стойност или модул на вектора на силата... Силовият модул се обозначава като или. Действието на силата върху тялото се проявява или в деформацията му, ако тялото е неподвижно, или в придаване на ускорение, когато тялото се движи. На тези прояви на сила се основава устройството на различни уреди (силомери или динамометри) за измерване на сили.
б) система от сили
Съвкупността от разглеждани сили се оформя система от сили.Всяка система, състояща се от n сили, може да се запише по следния начин: ![]()
в) свободно тяло
Тяло, което може да се движи в пространството във всяка посока, без да изпитва пряко (механично) взаимодействие с други тела, се нарича Безплатноили изолиран... Действието на една или друга система от сили върху тялото може да се изясни само ако това тяло е свободно.
г) резултантна сила
Ако някаква сила има същия ефект върху свободно тяло като определена система от сили, тогава тази сила се нарича резултатът от тази система от сили... Това е написано по следния начин:
![]() ,
,
което означава еквивалентностдействие върху едно и също свободно тяло на резултатната и някаква система от n сили.
Нека сега да пристъпим към разглеждане на по-сложни понятия, свързани с количественото определяне на ротационните ефекти на силите.
д) момент на сила около точка (център)
Ако тялото под действието на сила може да се върти около някаква неподвижна точка O (фиг. 2), то за количествено определяне на този ротационен ефект се въвежда физическа величина, която се нарича момент на сила около точка (център).

Нарича се равнината, минаваща през дадена фиксирана точка и линията на действие на силата равнината на действие на силата... На фиг. 2 това е равнината ОАВ.
Моментът на сила спрямо точка (център) е векторна величина, равна на векторното произведение на радиус вектора на точката на приложение на силата от вектора на силата:
![]() ( 1)
( 1)
Съгласно правилото за векторно умножение на два вектора, техният векторен продукт е вектор, перпендикулярен на равнината на разположение на векторите на факторите (в случая равнината на триъгълника OAB), насочен в посоката, от която е най-късият завъртането на първия вектор на фактора към втория вектор е факторът видими срещу стрелката на часовника (фиг. 2).При този ред на векторите на факторите на векторното произведение (1) въртенето на тялото под действието на силата ще се вижда срещу стрелката на часовника (фиг. 2) Тъй като векторът е перпендикулярен на равнината на действие на силата, нейното разположение в пространството определя положението на равнината на действие на силата.относно центъра е равно на удвоената площ ОАВ и може да се определи по формулата:
![]() ,
(2)
,
(2)
където величиназ, равно на най-краткото разстояние от дадена точка O до линията на действие на силата, се нарича рамо на силата.
Ако положението на равнината на действие на силата в пространството не е от съществено значение за характеристиката на въртеливото действие на силата, тогава в този случай да се характеризира ротационното действие на силата, вместо вектора на момента на силата , се използва алгебричен момент на сила:
![]() (3)
(3)
Алгебричният момент на сила спрямо даден център е равен на произведението на модула на силата от неговото рамо, взето със знак плюс или минус. В този случай положителният момент съответства на въртенето на тялото под действието на дадената сила срещу стрелката на часовника, а отрицателният момент съответства на въртенето на тялото по протежение на стрелката на часовника. От формули (1), (2) и (3) следва, че моментът на сила спрямо точката е нула само ако рамото на тази силазравно на нула... Такава сила не може да завърти тялото около дадена точка.
е) Момент на сила около оста
Ако тялото под действието на сила може да се върти около някаква фиксирана ос (например въртене на рамка на врата или прозорец в пантите, когато те са отворени или затворени), тогава за количествено определяне на този ротационен ефект се въвежда физическа величина, която е наречен момент на сила около дадена ос.
 z
z
б F xy
Фигура 3 показва диаграма, в съответствие с която се определя моментът на сила спрямо оста z:
Ъгълът се образува от две перпендикулярни посоки z и към равнините на триъгълници O аби OAV, съответно. Тъй като О абе проекцията на ОАВ върху xy равнината, тогава според стереометричната теорема за проекцията на плоска фигура върху тази равнина имаме:
където знакът плюс съответства на положителната стойност на cos, т.е. остри ъгли , а знакът минус отговаря на отрицателната стойност на cos, т.е. тъпи ъгли , което се дължи на посоката на вектора. От своя страна SO аб=1/2abh, където з аб ... Размер на сегмента абе равна на проекцията на силата върху равнината xy, т.е. . аб = Ф xy .
Въз основа на горното, както и на равенства (4) и (5), ние дефинираме момента на сила спрямо оста z, както следва:
Равенството (6) ни позволява да формулираме следната дефиниция на момента на сила спрямо която и да е ос: Моментът на сила спрямо дадена ос е равен на проекцията върху тази ос на вектора на момента на тази сила спрямо която и да е точка на тази ос и се определя като произведението на проекцията на силата върху равнината, перпендикулярна на тази ос, взета със знак плюс или минус на рамото на тази проекция спрямо точката на пресичане на оста с равнината на проекцията . В този случай знакът на момента се счита за положителен, ако гледайки от положителната посока на оста, въртенето на тялото около тази ос се вижда срещу стрелката на часовника. В противен случай моментът на сила около оста се приема като отрицателен. Тъй като това определение на момента на сила около оста е доста трудно за запомняне, се препоръчва да се запомни формулата (6) и фиг. 3, която обяснява тази формула.
От формула (6) следва, че моментът на сила около оста е нула, акотя е успоредна на оста (в този случай нейната проекция върху равнина, перпендикулярна на оста, е нула), или линията на действие на силата пресича оста (тогава рамото на проекцията з=0). Това напълно отговаря на физическия смисъл на момента на сила около оста като количествена характеристика на въртеливото действие на силата върху тяло с ос на въртене.
ж) телесно тегло
Отдавна е забелязано, че под действието на сила тялото набира скорост постепенно и продължава да се движи, ако силата бъде отстранена. Това свойство на телата да се противопоставят на промяната в движението им се наричаше инерция или инерция на телата. Количествената мярка за инертността на едно тяло е неговата маса.Освен това, телесната маса е количествена мярка за въздействието на гравитационните сили върху дадено тяло колкото по-голяма е масата на тялото, толкова по-голяма е гравитационната сила, действаща върху тялото.Както е показано по-долу, NSТези две определения за телесно тегло са свързани.
Останалите понятия и дефиниции на динамиката ще бъдат обсъдени по-късно в разделите, където се срещат за първи път.
2. Връзки и връзки на реакции
По-рано в раздел 1, точка (c), беше дадена концепцията за свободно тяло, като тяло, което може да се движи в пространството във всяка посока, без да е в пряк контакт с други тела. Повечето от реалните тела, които ни заобикалят, са в пряк контакт с други тела и не могат да се движат в една или друга посока. Така например телата върху повърхността на масата могат да се движат във всяка посока, с изключение на посоката, перпендикулярна на повърхността на масата надолу. Вратите с панти могат да се въртят, но не могат да се преместват и т. н. Телата, които не могат да се движат в пространството в една или друга посока се наричат не е безплатно.
Всичко, което ограничава движението на дадено тяло в пространството, се нарича ограничения.Това могат да бъдат всякакви други тела, които предотвратяват движението на това тяло в някои посоки ( физически връзки); в по-широк смисъл може да са някакви условия, наложени на движението на тялото, ограничаващи това движение. Така че можете да поставите условие, че движението на материална точка се извършва по дадена крива. В този случай връзката се определя математически под формата на уравнение ( ограничително уравнение). Въпросът за видовете връзки ще бъде разгледан по-подробно по-долу.
Повечето от връзките, наложени на телата, са практически физически връзки. Следователно възниква въпросът за взаимодействието на това тяло и връзката, наложена на това тяло. На този въпрос отговаря аксиомата за взаимодействието на телата: Две тела действат едно върху друго със сили, равни по големина, противоположни по посока и разположени на една и съща права линия. Тези сили се наричат сили на взаимодействие. Силите на взаимодействие се прилагат към различни взаимодействащи тела. Така например, при взаимодействието на дадено тяло и връзка, една от силите на взаимодействие се прилага от страната на тялото към връзката, а другата сила на взаимодействие се прилага от страната на връзката към това тяло. Тази последна мощност се нарича от силата на реакцията на връзкатаили просто, комуникационна реакция.
При решаване на практически задачи на динамиката е необходимо да можете да намерите посоката на реакциите на различни видове връзки. Общото правило за определяне на посоката на реакцията на връзката понякога може да помогне за това: Реакцията на връзката винаги е насочена обратно на посоката, в която тази връзка предотвратява движението на даденото тяло. Ако тази посока може да бъде определена, тогава реакцията на връзката ще бъде определена от посоката. В противен случай посоката на реакцията на връзката е несигурна и може да бъде намерена само от съответните уравнения на движение или равновесие на тялото. По-подробно въпросът за видовете връзки и посоката на техните реакции трябва да се проучи в учебника: S.M. Targ Кратък курс по теоретична механика "Гимназия", М., 1986 г. Глава 1, §3.
В раздел 1, точка (c) беше казано, че ефектът на всяка система от сили може да бъде напълно определен само ако тази система от сили се приложи към свободно тяло. Тъй като повечето тела в действителност не са свободни, тогава, за да се изследва движението на тези тела, възниква въпросът как да направим тези тела свободни. На този въпрос отговарят аксиома на лекционните връзки Нафилософия у дома. Лекциибяха ... социална психология и етнопсихология. 3. ТеоретиченРезултати В социалния дарвинизъм имаше...
Теоретичен механика
Учебно ръководство >> Физикаабстрактно лекции Напредмет ТЕОРЕТИЧНО МЕХАНИКАЗа студенти от специалност: 260501.65 ... - редовна форма Резюме лекциисъставено въз основа на: L.V. Butorin, E.B. Busygin. Теоретичен механика... Ръководство за обучение...
Във всеки академичен курс изучаването на физика започва с механика. Не от теоретична, не от приложна и не изчислителна, а от добрата стара класическа механика. Тази механика се нарича още Нютонова механика. Според легендата ученият се разхождал в градината, видял падаща ябълка и именно това явление го тласнало към откриването на закона за всемирното привличане. Разбира се, законът винаги е съществувал и Нютон му е дал само форма, която хората разбират, но заслугата му е безценна. В тази статия няма да описваме законите на Нютонова механика възможно най-подробно, но ще очертаем основите, основните знания, дефинициите и формулите, които винаги могат да ви играят на ръка.
Механиката е клон на физиката, наука, която изучава движението на материалните тела и взаимодействията между тях.
Самата дума е от гръцки произход и се превежда като „изкуството да се строят машини“. Но преди изграждането на машини, ние все още сме като Луната, така че ще вървим по стъпките на нашите предци и ще изучаваме движението на камъните, хвърлени под ъгъл към хоризонта, и ябълките, падащи върху глави от височина от з.

Защо изучаването на физиката започва с механика? Тъй като е напълно естествено, да не се стартира от термодинамично равновесие?!
Механиката е една от най-старите науки и исторически изучаването на физиката започва именно от основите на механиката. Поставени в рамките на времето и пространството, хората всъщност не биха могли да започнат от нещо друго, с цялото си желание. Движещите се тела са първото нещо, към което обръщаме внимание.
Какво е движение?
Механичното движение е промяна в положението на телата в пространството едно спрямо друго във времето.
След това определение съвсем естествено стигаме до концепцията за референтна рамка. Промяна на положението на телата в пространството едно спрямо друго.Ключови думи тук: един спрямо друг ... В крайна сметка пътник в кола се движи спрямо човек, стоящ отстрани на пътя с определена скорост, и почива спрямо съседа си на седалката до него и се движи с различна скорост спрямо пътник в кола, която ги изпреварва.

Ето защо, за да измерваме нормално параметрите на движещите се обекти и да не се объркаме, имаме нужда отправна система - твърдо свързани помежду си референтно тяло, координатна система и часовник. Например, Земята се движи около Слънцето в хелиоцентрична отправна система. В ежедневния живот ние извършваме почти всички наши измервания в геоцентрична референтна система, свързана със Земята. Земята е референтно тяло, спрямо което се движат автомобили, самолети, хора, животни.

Механиката като наука има своя задача. Задачата на механиката е да знае положението на тялото в пространството по всяко време. С други думи, механиката изгражда математическо описание на движението и намира връзки между физическите величини, които го характеризират.
За да продължим напред, имаме нужда от концепцията „ материална точка “. Казват, че физиката е точна наука, но физиците знаят колко приближения и предположения трябва да се направят, за да се споразумеят точно за тази точност. Никой никога не е виждал материална точка или мирише на идеален газ, но те са! Просто е много по-лесно да живееш с тях.
Материалната точка е тяло, чийто размер и форма могат да бъдат пренебрегнати в контекста на този проблем.
Раздели на класическата механика
Механиката се състои от няколко раздела
- Кинематика
- Динамика
- Статика
Кинематикаот физическа гледна точка изучава как точно се движи тялото. С други думи, този раздел се занимава с количествените характеристики на движението. Намерете скорост, път - типични кинематични проблеми
Динамикарешава въпроса защо се движи по този начин. Тоест, той отчита силите, действащи върху тялото.
Статикаизучава баланса на телата под действието на силите, тоест отговаря на въпроса: защо изобщо не пада?
Границите на приложимостта на класическата механика
Класическата механика вече не претендира да е наука, която обяснява всичко (в началото на миналия век всичко беше съвсем различно) и има ясна рамка за приложимост. Като цяло законите на класическата механика са валидни за света, с който сме свикнали по отношение на размерите (макрокосмоса). Те спират да работят в случая на света на частиците, когато квантовата механика заменя класическата. Също така класическата механика е неприложима за случаите, когато телата се движат със скорост, близка до скоростта на светлината. В такива случаи релативистичните ефекти стават ясно изразени. Грубо казано, в рамките на квантовата и релативистичната механика - класическата механика, това е специален случай, когато размерите на тялото са големи, а скоростта е малка.

Най-общо казано, квантовите и релативистичните ефекти никога не отиват никъде; те също се случват при обикновеното движение на макроскопични тела със скорост, много по-малка от скоростта на светлината. Друго нещо е, че ефектът от тези ефекти е толкова малък, че не надхвърля най-точните измервания. Така класическата механика никога няма да загуби своето основно значение.
Ще продължим да изучаваме физическите основи на механиката в бъдещи статии. За по-добро разбиране на механиката, винаги можете да се обърнете към на нашите автори които поотделно хвърлят светлина върху тъмното петно на най-трудната задача.
1 слайд
Курс на лекции по теоретична механика Динамика (I част) Бондаренко A.N. Москва - 2007 Електронният учебен курс е написан на базата на лекциите, изнесени от автора за студенти, учили в специалностите на SZD, PGS и SDM в НИИЖТ и МИИТ (1974-2006). Учебният материал отговаря на календарните планове в обем от три семестъра. За да приложите напълно анимационните ефекти по време на презентация, трябва да използвате програма за преглед на Power Point не по-ниска от тази, вградена в Microsoft Office на операционната система Windows-XP Professional. Коментарите и предложенията могат да бъдат изпращани по имейл: [защитен с имейл]... Московски държавен железопътен университет (MIIT) Катедра по теоретична механика Научно-технически център за транспортни технологии

2 слайд
Съдържание Лекция 1. Въведение в динамиката. Закони и аксиоми на динамиката на материална точка. Основно уравнение на динамиката. Диференциални и естествени уравнения на движението. Две основни задачи на динамиката. Примери за решаване на директната задача на динамиката Лекция 2. Решение на обратната задача на динамиката. Общи указания за решаване на обратната задача на динамиката. Примери за решаване на обратната задача на динамиката. Движението на тяло, хвърлено под ъгъл спрямо хоризонта, без да се отчита съпротивлението на въздуха. Лекция 3. Праволинейни трептения на материална точка. Условие за възникване на вибрации. Класификация на вибрациите. Свободни вибрации без да се вземат предвид силите на съпротивление. Затихване на трептения. Намаляване на флуктуациите. Лекция 4. Принудителни трептения на материална точка. Резонанс. Ефектът на съпротивлението на движение по време на принудителни вибрации. Лекция 5. Относително движение на материална точка. Инерционни сили. Конкретни случаи на движение за различни видове преносими движения. Влиянието на въртенето на Земята върху баланса и движението на телата. Лекция 6. Динамика на механична система. Механична система. Външни и вътрешни сили. Центърът на масата на системата. Теорема за движението на центъра на масите. Закони за опазване. Пример за решаване на задачата с помощта на теоремата за движението на центъра на масата. Лекция 7. Импулс на властта. Количеството движение. Теоремата за промяната в количеството на движението. Закони за опазване. Теорема на Ойлер. Пример за решаване на проблема за използване на теоремата за промяна на импулса. Момент на инерция. Теорема за изменението на ъгловия импулс .. Лекция 8. Закони за запазване. Елементи на теорията на инерционните моменти. Кинетичен момент на твърдо тяло. Диференциално уравнение на въртене на твърдо тяло. Пример за решаване на задачата за използването на теоремата за промяната на ъгловия импулс на системата. Елементарна теория на жироскопа. Препоръчителна литература 1. Yablonsky A.A. Теоретичен курс по механика. Част 2. М .: Висше училище. 1977 368 с. 2. Мешчерски И.В. Сборник задачи по теоретична механика. М.: Наука. 1986 416 с. 3. Сборник със задачи за курсови работи / Изд. А.А. Яблонски. М.: Висше училище. 1985 366 стр. 4. Бондаренко А. Н. „Теоретична механика в примери и задачи. Динамика ”(електронно ръководство www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004 г.

3 слайд
Лекция 1 Динамиката е клон на теоретичната механика, който изучава механичното движение от най-обща гледна точка. Движението се разглежда във връзка със силите, действащи върху обекта. Разделът се състои от три раздела: Динамика на материална точка Динамика на механична система Аналитична механика ■ Динамика на точка – изучава движението на материална точка, като се вземат предвид силите, които предизвикват това движение. Основният обект е материална точка - материално тяло с маса, чиито размери могат да бъдат пренебрегнати. Основни допускания: - има абсолютно пространство (то има чисто геометрични свойства, които не зависят от материята и нейното движение. - има абсолютно време (не зависи от материята и нейното движение). Оттук следва: - има абсолютно неподвижно референтна система - времето не зависи от движението на референтната система - масите на движещите се точки не зависят от движението на референтната система Тези предположения се използват в класическата механика, създадена от Галилей и Нютон. Той все още има доста широко поле на приложение, тъй като механичните системи, разглеждани в приложните науки, нямат толкова големи маси и скорости на движение, за които е необходимо да се вземе предвид тяхното влияние върху геометрията на пространството, времето, движението, както се прави в релативистичната механика (теория на относителността).динамичното им взаимодействие Действия под въздействието на различни сили. ■ Законът за инерцията (законът на Галилео-Нютон) - Изолирана материална точка, тялото запазва състоянието си на покой или равномерно праволинейно движение, докато приложените сили не го принудят да промени това състояние. Това предполага еквивалентност на състоянието на покой и движение по инерция (законът за относителността на Галилей). Референтната система, по отношение на която се изпълнява законът за инерцията, се нарича инерционна. Свойството на материалната точка да се стреми да запази скоростта на своето движение (кинематичното си състояние) непроменена се нарича инерция. ■ Законът за пропорционалността на силата и ускорението (Основно уравнение на динамиката - законът на Нютон II) - Ускорението, придадено на материална точка чрез сила, е право пропорционално на силата и обратно пропорционално на масата на тази точка: или Тук m е маса на точката (мярка за инерция), измерена в kg, числено равно тегло, разделено на ускорението на гравитацията: F е действащата сила, измерена в N (1 N придава ускорение от 1 m / s2 на точка с тегло 1 kg , 1 N = 1/9. 81 kg-s). ■ Динамика на механична система – изучава движението на съвкупност от материални точки и твърди тела, обединени от общи закони на взаимодействие, като се вземат предвид силите, които предизвикват това движение. ■ Аналитична механика – изучава движението на несвободни механични системи с помощта на общи аналитични методи. 1

4 слайд
Лекция 1 (продължение - 1.2) Диференциални уравнения на движение на материална точка: - диференциално уравнение на движение на точка във векторна форма. - диференциални уравнения на движение на точка в координатна форма. Този резултат може да бъде получен чрез формална проекция на векторното диференциално уравнение (1). След групирането, векторната връзка се разпада на три скаларни уравнения: В координатна форма: Използваме връзката на радиус вектора с координати и вектора на силата с проекции: или: Заменяме ускорението на точка във векторната настройка на движение в основно уравнение на динамиката: Естествените уравнения на движението на материална точка се получават чрез проектиране на векторно диференциално уравнение на движение върху естествени (подвижни) координатни оси: или: - естествени уравнения на движение на точка. ■ Основното уравнение на динамиката: - съответства на векторния метод за определяне на движението на точка. ■ Законът за независимост на действието на силите - Ускорението на материална точка под действието на няколко сили е равно на геометричната сума от ускоренията на точка от действието на всяка от силите поотделно: или Законът е валиден за всяко кинематично състояние на телата. Силите на взаимодействие, приложени към различни точки (тела), не са балансирани. ■ Законът за равенството на действието и реакцията (III закон на Нютон) - Всяко действие съответства на равна по големина и противоположно насочена реакция: 2

5 слайд
Два основни проблема на динамиката: 1. Директен проблем: Дава се движение (уравнения на движение, траектория). Необходимо е да се определят силите, под чието действие се осъществява дадено движение. 2. Обратна задача: Силите, под чието действие се осъществява движението. Необходимо е да се намерят параметрите на движението (уравнения на движение, траектория на движение). И двете задачи се решават с помощта на основното уравнение на динамиката и неговата проекция върху координатните оси. Ако се разглежда движението на несвободна точка, тогава, както в статиката, се използва принципът на свобода от връзки. В резултат на реакцията връзките се включват в състава на силите, действащи върху материалната точка. Решението на първия проблем е свързано с операции за диференциране. Решаването на обратната задача изисква интегриране на съответните диференциални уравнения, а това е много по-трудно от диференцирането. Обратната задача е по-сложна от директната. Нека разгледаме решението на директната задача за динамиката чрез примери: Пример 1. Кабина на асансьор с тегло G се повдига от въже с ускорение a. Определете напрежението на кабела. 1. Избираме обект (кабината на асансьора се движи напред и може да се разглежда като материална точка). 2. Изхвърляме връзката (кабела) и заменяме с реакция R. 3. Съставяме основното уравнение на динамиката: Определяме реакцията на кабела: Определяме напрежението на кабела: При равномерно движение на кабината ay = 0 и напрежението на кабела е равно на тежестта: T = G. Когато кабелът се скъса, T = 0 и ускорението на автомобила е равно на ускорението на гравитацията: ay = -g. 3 4. Да проектираме основното уравнение на динамиката върху оста y: y Пример 2. Точка с маса m се движи по хоризонтална повърхност (равнина Oxy) съгласно уравненията: x = a coskt, y = b coskt. Определете силата, действаща върху точката. 1. Изберете обект (материална точка). 2. Изхвърляме връзката (равнината) и я заместваме с реакция N. 3. Добавяме неизвестната сила F. към системата от сили 4. Съставяме основното уравнение на динамиката: 5. Проектираме основното уравнение на динамиката върху оси x, y: Определяме проекциите на силата: Силов модул: Косинус на посоката: По този начин големината на силата е пропорционална на разстоянието на точката до центъра на координатите и е насочена към центъра по линията, свързваща сочи към центъра. Траекторията на точка е елипса с център в началото: O r Лекция 1 (продължение - 1.3)

6 слайд
Лекция 1 (продължение 1.4) Пример 3: Товар с тежест G е окачен на въже с дължина l и се движи по кръгова пътека в хоризонтална равнина с определена скорост. Ъгълът на отклонение на кабела от вертикалата е равен. Определете напрежението на въжето и скоростта на натоварване. 1. Изберете обекта (товара). 2. Изхвърляме връзката (кабела) и заменяме с реакция R. 3. Съставяме основното уравнение на динамиката: От третото уравнение определяме реакцията на кабела: Определяме напрежението на кабела: Заменяме стойността на кабелна реакция, нормално ускорение във второто уравнение и определяне на скоростта на товара: 4. Проектиране на динамиката на основното уравнение върху оста, n, b: Пример 4: Автомобил с тегло G се движи по изпъкнал мост (радиус на кривина е R) при скорост V. Определете налягането на автомобила върху моста. 1. Изберете обект (автомобил, пренебрегнете размерите му и го разгледайте като точка). 2. Изхвърляме връзката (груба повърхност) и заместваме с реакции N и сила на триене Ffr. 3. Съставяме основното уравнение на динамиката: 4. Проектираме основното уравнение на динамиката върху оста n: От тук определяме нормалната реакция: Определяме налягането на автомобила върху моста: От тук можем да определим скоростта съответстващо на нулево налягане върху моста (Q = 0): 4

7 слайд
Лекция 2 След заместване на намерените стойности на константите получаваме: Така под действието на една и съща система от сили материална точка може да извърши цял клас движения, определени от началните условия. Началните координати отчитат първоначалната позиция на точката. Началната скорост, дадена от проекциите, отчита влиянието върху нейното движение по разглеждания участък от траекторията на силите, действащи върху точката, преди да пристигнат в този участък, т.е. начално кинематично състояние. Решение на обратната задача на динамиката - В общия случай движението на точка на сила, действаща върху точка, са променливи, които зависят от времето, координатите и скоростта. Движението на точка се описва със система от три диференциални уравнения от втори ред: След интегриране на всяко от тях, ще има шест константи C1, C2,…., C6: Стойностите на константите C1, C2,… ., C6 се намират от шест начални условия при t = 0: Решение, пример 1, обратна задача: Свободна материална точка с маса m се движи под действието на сила F, постоянна по големина и величина. ... В началния момент скоростта на точката е v0 и съвпада по посока със силата. Определете уравнението на движението на точка. 1. Съставете основното уравнение на динамиката: 3. Намалете реда на производната: 2. Изберете декартова референтна система, насочвайки оста x по посока на силата и проектирайте основното уравнение на динамиката върху тази ос: или xyz 4. Разделете променливите: 5. Изчислете интегралите от двете страни на уравнението: 6. Представяме проекцията на скоростта като производна на координатата по отношение на времето: 8. Изчисляваме интегралите от двете страни на уравнението: 7. Разделете променливите: 9. За да определим стойностите на константите C1 и C2, използваме началните условия t = 0, vx = v0, x = x0: В резултат получаваме уравнението на равномерно движение (по оста x): 5

8 слайд
Общи инструкции за решаване на директна и обратна задача. Процедура за решаване: 1. Съставяне на диференциалното уравнение на движение: 1.1. Изберете координатна система - правоъгълна (фиксирана) с неизвестна траектория на движение, естествена (подвижна) с известна траектория, например окръжност или права линия. В последния случай може да се използва една праволинейна координата. Подравнете началото с началната позиция на точката (при t = 0) или с равновесното положение на точката, ако съществува, например, когато точката вибрира. 6 1.2. Начертайте точка в позиция, съответстваща на произволен момент от времето (за t> 0), така че координатите да са положителни (s> 0, x> 0). В този случай приемаме също, че проекцията на скоростта в това положение също е положителна. В случай на трептения проекцията на скоростта променя знака, например при връщане в положение на равновесие. Тук трябва да се приеме, че в разглеждания момент от време точката се отдалечава от положението на равновесие. Тази препоръка е важна в бъдеще при работа със съпротивителни сили, зависими от скоростта. 1.3. Освободете материалната точка от връзки, заменете тяхното действие с реакции, добавете активни сили. 1.4. Запишете основния закон на динамиката във векторна форма, проектирайте върху избраните оси, изразете дадените или реактивни сили чрез времеви променливи, координати или скорости, ако те зависят от тях. 2. Решение на диференциални уравнения: 2.1. Намалете производната, ако уравнението не е сведено до каноничната (стандартна) форма. например: или 2.2. Разделени променливи, например: или 2.4. Изчислете неопределени интеграли от лявата и дясната страна на уравнението, например: 2.3. Ако в уравнението има три променливи, тогава направете промяна на променливите, например: и след това разделете променливите. Коментирайте. Вместо да изчислявате неопределени интеграли, можете да изчислите определени интеграли с променлива горна граница. Долните граници представляват началните стойности на променливите (начални условия). Тогава не се изисква отделно определяне на константата, която автоматично се включва в решението, например: Използвайки началните условия, например, t = 0 , vx = vx0, определете константата на интегриране: 2.5. Изразете скоростта по отношение на производната на координатите във времето, например, и повторете параграфи 2.2-2.4. Забележка. Ако уравнението се сведе до каноничната форма, която има стандартно решение, тогава се използва това готово решение. Интеграционните константи все още се намират от началните условия. Вижте например колебание (Лекция 4, стр. осем). Лекция 2 (продължение 2.2)

9 слайд
Лекция 2 (продължение 2.3) Пример 2 за решаване на обратната задача: Силата зависи от времето. Товар с тежест P започва да се движи по гладка хоризонтална повърхност под действието на сила F, чиято стойност е пропорционална на времето (F = kt). Определете разстоянието, изминато от товара за време t. 3. Съставете основното уравнение на динамиката: 5. Намалете реда на производната: 4. Проектирайте основното уравнение на динамиката върху оста x: или 7 6. Разделете променливите: 7. Изчислете интегралите от двете страни на уравнението: 9. Нека представим проекцията на скоростта като производна по време на координатата: 10. Изчислете интегралите от двете страни на уравнението: 9. Разделете променливите: 8. Определете стойността на константата C1 от начално условие t = 0, vx = v0 = 0: В резултат получаваме уравнението на движението (по оста x), което дава стойността на изминатото разстояние за време t: 1. Изберете референтна система ( Декартови координати), така че тялото да има положителна координата: 2. Приемаме обекта на движение като материална точка (тялото се движи напред), освобождаваме го от връзката (референтна равнина) и го заменяме с реакция (нормална реакция на гладка повърхност) : 11. Определете стойността на константата C2 от началното условие t = 0, x = x0 = 0: Пример 3 за решаване на обратната задача: Силата зависи от координатата. Материална точка с маса m се изхвърля нагоре от повърхността на Земята със скорост v0. Гравитацията на Земята е обратно пропорционална на квадрата на разстоянието от точка до центъра на тежестта (центъра на Земята). Определете зависимостта на скоростта от разстоянието y до центъра на Земята. 1. Избираме референтна система (декартови координати), така че тялото да има положителна координата: 2. Съставяме основното уравнение на динамиката: 3. Проектираме основното уравнение на динамиката върху оста y: или Коефициентът на пропорционалността може да бъде намерена с помощта на теглото на точка от повърхността на Земята: R Оттук диференциалът на уравнението изглежда така: или 4. Намалете реда на производната: 5. Направете промяната на променливата: 6. Разделете променливите : 7. Изчислете интегралите от двете страни на уравнението: 8. Заменете границите: В резултат получаваме израза за скоростта като функция на y-координата: Максималната скорост на полета на височина може да бъде намерена чрез приравняване на скоростта до нула: Максимална височина на полета, когато знаменателят изчезне: Следователно, когато се задава радиусът на Земята и гравитационното ускорение, се получава II космическа скорост:

10 слайд
Лекция 2 (продължение 2.4) Пример 2 за решаване на обратната задача: Силата зависи от скоростта. Кораб с маса m имаше скорост v0. Съпротивлението на водата спрямо движението на съда е пропорционално на скоростта. Определете времето, през което скоростта на лодката ще спадне наполовина след изключване на двигателя, както и разстоянието, изминато от лодката до пълно спиране. 8 1. Избираме референтна система (декартови координати), така че тялото да има положителна координата: 2. Приемаме обекта на движение като материална точка (корабът се движи напред), освобождаваме го от връзките (вода) и заменете го с реакция (плаваема сила - силата на Архимед), а също и със силата на съпротива на движение. 3. Добавете активна сила (гравитация). 4. Съставете основното уравнение на динамиката: 5. Проектирайте основното уравнение на динамиката върху оста x: или 6. Намалете реда на производната: 7. Разделете променливите: 8. Изчислете интегралите от двете страни на уравнение: 9. Заменете границите: Получава се израз, който свързва скоростта и времето t, откъдето можете да определите времето на движение: Времето на движение, през което скоростта ще спадне наполовина: Интересно е да се отбележи, че когато скоростта се доближи до нула, времето на движение клони към безкрайност, т.е крайната скорост не може да бъде нула. Не е ли "вечно движение"? Въпреки това, изминатото разстояние до спирката е крайната стойност. За да определим изминатото разстояние, се обръщаме към израза, получен след понижаване на реда на производната, и правим промяната на променливата: След интегриране и заместване на границите, получаваме: Изминатото разстояние до спирката: ■ Движението на точка, хвърлена под ъгъл спрямо хоризонта в хомогенно гравитационно поле, без да се отчита съпротивлението на въздуха. Елиминирайки времето от уравненията на движението, получаваме уравнението на траекторията: Времето на полета се определя чрез приравняване на координатата y на нула: Обхватът на полета се определя чрез заместване на полетното време:

11 слайд
Лекция 3 Праволинейни трептения на материална точка - Осцилаторното движение на материална точка възниква при условие: има възстановяваща сила, която се стреми да върне точката в равновесно положение при всяко отклонение от това положение. 9 Има възстановяваща сила, равновесното положение е стабилно Няма възстановяваща сила, положението на равновесие е нестабилно Няма възстановяваща сила, равновесното положение е безразлично. Тя винаги е насочена към положение на равновесие, стойността е право пропорционална на линейното удължение (скъсяване) на пружината, равна на отклонението на тялото от равновесното положение: c е коефициентът на твърдост на пружината, числено равен на силата при което пружината променя дължината си с единица, измерена в N / m в системата SI. x y O Видове вибрации на материална точка: 1. Свободни вибрации (без да се отчита съпротивлението на средата). 2. Свободни вибрации, като се отчита съпротивлението на средата (затихващи вибрации). 3. Принудителни вибрации. 4. Принудителни вибрации, като се отчита съпротивлението на средата. ■ Свободни вибрации - възникват под действието само на възстановяващата сила. Нека запишем основния закон на динамиката: Изберете координатна система, центрирана в позицията на равновесие (точка O) и проектирайте уравнението върху оста x: Нека сведем полученото уравнение до стандартната (канонична) форма: Това уравнение е хомогенно линейно диференциално уравнение от втори ред, чиято форма на решение се определя от корените на характеристиката уравнението, получено с помощта на универсалното заместване: Корените на характеристичното уравнение са въображаеми и равни: Общото решение на диференциалното уравнение има вида: Точкова скорост: Начални условия: Определете константите: И така, уравнението на свободните трептения има вида: Уравнението може да бъде представено с едночленен израз: - начална фаза. Новите константи a и - са свързани с константите C1 и C2 чрез отношенията: Да определим a и: Причината за възникване на свободни трептения е началното преместване x0 и/или началната скорост v0.

12 слайд
10 Лекция 3 (продължение 3.2) Затихване на трептения на материална точка - Осцилаторното движение на материална точка възниква при наличие на възстановяваща сила и сила на съпротивление на движение. Зависимостта на силата на съпротивление на движение от преместването или скоростта се определя от физическата природа на средата или връзката, която предотвратява движението. Най-простата зависимост е линейна зависимост от скоростта (вискозно съпротивление): - коефициент на вискозитет xy O Основно уравнение на динамиката: Проекция на уравнението на динамиката върху оста: Нека приведем уравнението до стандартен вид: където Характеристичното уравнение има корени : Общото решение на това диференциално уравнение има различна форма в зависимост от стойностите на корените: 1.n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - случай на висока вискозна устойчивост: - истински корени, различни. или - тези функции са апериодични: 3. n = k: - реални, кратни корени. тези функции също са апериодични:

13 слайд
Лекция 3 (продължение 3.3) Класификация на решенията на свободните трептения. Методи за свързване на пружини. Еквивалентна твърдост. y y 11 Диф. уравнение Характер. уравнение корени характер. уравнения Решение на диференциалното уравнение Графика nk n = k

14 слайд
Лекция 4 Принудителни вибрации на материална точка - Заедно с възстановяващата сила действа и периодично променяща се сила, наречена смущаваща сила. Смущаващата сила може да бъде от различно естество. Например, в конкретен случай инерционният ефект на небалансираната маса m1 на въртящ се ротор причинява хармонично променящи се проекции на силата: Основно уравнение на динамиката: Проекция на уравнението на динамиката върху ос: Нека приведем уравнението до стандартна форма: 12 Решението на това нехомогенно диференциално уравнение се състои от две части x = x1 + x2: x1 е общото решение на съответното хомогенно уравнение и x2 е конкретното решение на нехомогенното уравнение: Избираме конкретното решение във формата от дясната страна: Полученото равенство трябва да бъде изпълнено за всяко t. Тогава: или Така, при едновременното действие на възстановяващите и смущаващите сили, материалната точка извършва сложно колебателно движение, което е резултат от добавянето (суперпозицията) на свободни (x1) и принудителни (x2) трептения. Ако п< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (принудени трептения с висока честота), тогава фазата на трептенията е противоположна на фазата на смущаващата сила:

15 слайд
Лекция 4 (продължение 4.2) 13 Динамичният коефициент е съотношението на амплитудата на принудителните вибрации към статичното отклонение на точка под действието на постоянна сила H = const: Амплитуда на принудителните вибрации: Статичното отклонение може да се намери от равновесно уравнение: Тук: Оттук: Така, в p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (висока честота на принудителните вибрации) динамичен коефициент: Резонанс – възниква, когато честотата на принудителното трептене съвпада с честотата на собствените вибрации (p = k). Това най-често се случва при стартиране и спиране на въртене на лошо балансирани ротори, прикрепени към еластични окачвания. Диференциалното уравнение на трептения с еднакви честоти: Конкретното решение под формата на дясната страна не може да бъде взето, тъй като получавате линейно зависимо решение (вижте общото решение). Общо решение: Заместете в диференциалното уравнение: Вземете конкретно решение във формата и изчислете производните: Така се получава решението: или Принудителните трептения при резонанс имат амплитуда, която нараства неограничено пропорционално на времето. Ефектът на съпротивлението на движение по време на принудителни вибрации. Диференциалното уравнение при наличие на вискозно съпротивление има вида: Общото решение се избира от таблицата (Лекция 3, стр. 11), в зависимост от съотношението на n и k (виж). Нека вземем конкретното решение във формата и да изчислим производните: Заместване в диференциалното уравнение: Приравнявайки коефициентите за едни и същи тригонометрични функции, получаваме системата от уравнения: Повишаваме двете уравнения на степен и ги добавяме към степента на двете уравнения, получаваме амплитудата на принудителните трептения: Като разделим второто уравнение на първото, получаваме фазовото изместване на принудителните трептения: Така, уравнението на движението за принудителни вибрации, като се вземе предвид съпротивлението на движение, напр. , за n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 слайд
Лекция 5 Относително движение на материална точка – Да предположим, че движещата се (неинерциална) координатна система Oxyz се движи по определен закон спрямо неподвижната (инерционна) координатна система O1x1y1z1. Движението на материалната точка M (x, y, z) спрямо движещата се система Oxyz е относително, спрямо неподвижната система O1x1y1z1 е абсолютно. Движението на мобилната система Oxyz спрямо стационарната система O1x1y1z1 е преносимо движение. 14 z x1 y1 z1 O1 xy M xyz O Основно уравнение на динамиката: Абсолютно ускорение на точка: Заместете абсолютното ускорение на точка в основното уравнение на динамиката: Прехвърляне на термини с транслационно и Кориолисово ускорение към дясната страна: Прехвърлените членове имат размерността на силите и се считат за съответните инерционни сили, равни: Тогава относителното движение на точка може да се счита за абсолютно, ако добавим към действащите сили транслационните и кориолисовите сили на инерцията: В проекциите върху оста на движещата се координатна система, имаме: въртенето е равномерно, тогава εe = 0: 2. Транслационно криволинейно движение: Ако движението е праволинейно, тогава =: Ако движението е праволинейно и равномерно, тогава движещата се система е инерционна и относителната движението може да се счита за абсолютно: движение (принципът на относителността на класическата механика). Влияние на въртенето на Земята върху баланса на телата – Да приемем, че тялото е в равновесие на повърхността на Земята на произволна ширина φ (успоредна). Земята се върти около оста си от запад на изток с ъглова скорост: Радиусът на Земята е около 6370 km. S R - пълна реакция на негладка повърхност. G е силата на гравитацията на Земята към центъра. Ф - центробежна сила на инерцията. Условие на относително равновесие: Резултатът от силите на привличане и инерция е силата на гравитацията (теглото): Величината на силата на гравитацията (теглото) върху повърхността на Земята е P = mg. Центробежната сила на инерцията е малка част от силата на гравитацията: Отклонението на силата на гравитацията от посоката на силата на гравитацията също е малко: По този начин влиянието на въртенето на Земята върху баланса на телата е изключително малък и не се взема предвид при практическите изчисления. Максималната стойност на силата на инерцията (при φ = 0 - при екватора) е само 0,00343 от стойността на силата на гравитацията

17 слайд
Лекция 5 (продължение 5.2) 15 Влияние на въртенето на Земята върху движението на телата в земното гравитационно поле - Нека тялото падне на Земята от определена височина H над земната повърхност на географска ширина φ. Нека изберем движеща се отправна система, неподвижно свързана със Земята, насочвайки осите x, y тангенциално към паралела и меридиана: Така силата на гравитацията се отъждествява със силата на гравитацията. Освен това приемаме, че силата на гравитацията е насочена перпендикулярно на повърхността на Земята поради малкото отклонение, както беше обсъдено по-горе. Ускорението на Кориолис е равно и насочено успоредно на оста y на запад. Инерционната сила на Кориолис е равна на обратната посока. Нека проектираме уравнението на относителното движение върху оста: Решението на първото уравнение дава: Начални условия: Решението на третото уравнение дава: Начални условия: Третото уравнение има формата: Начални условия: Решението му дава: Полученото решение показва, че тялото се отклонява на изток при падане. Нека изчислим стойността на това отклонение, например при падане от височина 100 м. Времето на падането се намира от решението на второто уравнение: По този начин влиянието на въртенето на Земята върху движението на телата е изключително малък за практически височини и скорости и не се взема предвид при техническите изчисления. Решението на второто уравнение също предполага наличието на скорост по оста y, която също трябва да предизвика и предизвика съответното ускорение и инерционната сила на Кориолис. Ефектът от тази скорост и силата на инерцията, свързана с нея, върху промяната в движението ще бъде дори по-малък от разглежданата инерционна сила на Кориолис, свързана с вертикалната скорост.

18 слайд
Лекция 6 Динамика на механична система. Система от материални точки или механична система - Съвкупност от материални точки или материални точки, обединени от общи закони на взаимодействие (положението или движението на всяка от точките или тялото зависи от позицията и движението на всички останали) Система на свободни точки - движението на които не е ограничено от никакви връзки (например планетарна система, в която планетите се считат за материални точки). Система от несвободни точки или несвободна механична система - движението на материални точки или тела е ограничено от ограниченията, наложени на системата (например механизъм, машина и т.н.). 16 Сили, действащи върху системата. В допълнение към съществуващата преди това класификация на силите (активни и реактивни сили) се въвежда нова класификация на силите: 1. Външни сили (д) - действащи върху точките и телата на системата от точките или телата, които не са част на тази система. 2. Вътрешни сили (i) - сили на взаимодействие между материални точки или тела, включени в тази система. Една и съща сила може да бъде както външна, така и вътрешна сила. Всичко зависи от това коя механична система се разглежда. Например: В системата на Слънцето, Земята и Луната всички гравитационни сили между тях са вътрешни. Когато разглеждаме системата Земята и Луната, гравитационните сили, приложени от Слънцето, са външни: C З Л Въз основа на закона за действието и реакцията всяка вътрешна сила Fk съответства на друга вътрешна сила Fk ', равна по величина и противоположна по посока. От това следват две забележителни свойства на вътрешните сили: Главният вектор на всички вътрешни сили на системата е равен на нула: Основният момент на всички вътрешни сили на системата спрямо всеки център е равен на нула: Или в проекции върху координатата оси: Забележка. Въпреки че тези уравнения са подобни на уравненията на равновесието, те не са, тъй като вътрешните сили се прилагат към различни точки или тела на системата и могат да накарат тези точки (тела) да се движат една спрямо друга. От тези уравнения следва, че вътрешните сили не влияят на движението на системата, разглеждана като цяло. Центърът на масата на системата от материални точки. За да се опише движението на системата като цяло, се въвежда геометрична точка, наречена център на масата, чийто радиус вектор се определя от израза, където M е масата на цялата система: Или в проекции върху координатата оси: Формулите за центъра на масата са подобни на формулите за центъра на тежестта. Концепцията за центъра на масата обаче е по-обща, тъй като не е свързана с гравитационни сили или гравитационни сили.

19 слайд
Лекция 6 (продължение 6.2) 17 Теорема за движението на центъра на масата на системата - Разгледайте система от n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултантни Fke и Fki. Нека запишем за всяка точка основното уравнение на динамиката: или Сумираме тези уравнения за всички точки: От лявата страна на уравнението въвеждаме масите под знака на производната и заменяме сумата от производните с производната от сумата: От определението на центъра на масата: Заместете в полученото уравнение: получаваме или: Произведението на масата на системата и ускорението на нейния център, масата е равна на главния вектор на външните сили. В проекции върху координатните оси: Центърът на масата на системата се движи като материална точка с маса, равна на масата на цялата система, към която се прилагат всички външни сили, действащи върху системата. Последици от теоремата за движението на центъра на масата на системата (закони за запазване): 1. Ако във времевия интервал главният вектор на външните сили на системата е равен на нула, Re = 0, то скоростта на центърът на масата е постоянен, vC = const (центърът на масата се движи равномерно праволинейно - законът за запазване на центъра на движението на масата). 2. Ако във времевия интервал проекцията на главния вектор на външните сили на системата върху оста x е равна на нула, Rxe = 0, тогава скоростта на центъра на масата по оста x е постоянна, vCx = const (центърът на масата се движи равномерно по оста). Подобни твърдения са верни за осите y и z. Пример: Двама души с маси m1 и m2 са в лодка с маса m3. В началния момент лодката с хора почива. Определете движението на лодката, ако човек с тегло m2 се е преместил до носа на лодката на разстояние a. 3. Ако във времевия интервал главният вектор на външните сили на системата е равен на нула, Re = 0, а в началния момент скоростта на центъра на масата е нула, vC = 0, то радиус векторът на центърът на масата остава постоянен, rC = const (центърът на масата е в покой - законът за запазване на положението на центъра на масата). 4. Ако в интервала от време проекцията на главния вектор на външните сили на системата върху оста x е нула, Rxe = 0, а в началния момент скоростта на центъра на масата по тази ос е нула, vCx = 0, тогава координатата на центъра на масата по оста x остава постоянна, xC = const (центърът на масата не се движи по тази ос). Подобни твърдения са верни за осите y и z. 1. Обект на движение (лодка с хора): 2. Изхвърляме връзки (вода): 3. Заменяме връзката с реакция: 4. Добавете активни сили: 5. Запишете теоремата за центъра на масата: Проектирайте върху x -ос: O Определете колко далеч да смените местата до човек с маса m1, така че лодката да остане на място: Лодката ще се премести на разстояние l в обратна посока.

20 слайд
Лекция 7 Силов импулс - мярка за механично взаимодействие, характеризираща прехвърлянето на механичното движение от страната на силите, действащи върху точка за даден период от време: 18 до точка на сила за същия период от време: Умножете по dt : Ще интегрираме за даден интервал от време: Количеството движение на точка е мярка за механично движение, определено от вектор, равен на произведението на масата на точка от вектора на нейната скорост: Теорема за промяната в количеството движение на системата - Разгледайте системата n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултантни Fke и Fki. Нека запишем за всяка точка основното уравнение на динамиката: или Броят на движението на системата от материални точки е геометричната сума от количествата на движението на материалните точки: По дефиниция на центъра на масата: Векторът на импулса на системата е равно на произведението на масата на цялата система от вектора на скоростта на центъра на масата на системата. Тогава: В проекции върху координатните оси: Производната на вектора на импулса на системата по отношение на времето е равна на главния вектор на външните сили на системата. Нека обобщим тези уравнения върху всички точки: От лявата страна на уравнението въвеждаме масите под знака на производната и заменяме сбора на производните с производната на сумата: От дефиницията на импулса на системата : В проекции върху координатните оси:

21 слайд
Теорема на Ойлер - Приложение на теоремата за промяната на импулса на системата към движението на непрекъсната среда (вода). 1. Избираме обема на водата в криволинейния канал на турбината като обект на движение: 2. Отхвърляме ограниченията и заменяме тяхното действие с реакции (Rпов - резултатът от повърхностните сили) 3. Добавяме активни сили (Rпов - резултантът на обемните сили): 4. Запишете теоремата за промяната в количеството движение на системата: Количеството движение на водата в моменти t0 и t1 се представя като сбор: Промяна в количеството движение на водата в интервалът от време: Промяна в количеството движение на водата за безкрайно малък интервал от време dt:, където F1 F2 Като вземем произведението на плътността, площта на напречното сечение и скоростта за втора маса, получаваме: Замествайки диференциала на импулса на системата в теорема за промяна, получаваме: Последици от теоремата за промяната в импулса на системата (закони за запазване): 1. Ако във времевия интервал главният вектор на външните сили на системата е равен на нула, Re = 0, то векторът на количеството на движението е постоянен, Q = const е законът за запазване на импулса на системата). 2. Ако във времевия интервал проекцията на главния вектор на външните сили на системата върху оста x е равна на нула, Rxe = 0, то проекцията на импулса на системата върху оста x е постоянна , Qx = const. Подобни твърдения са верни за осите y и z. Лекция 7 (продължение 7.2) Пример: Граната с маса M, летяща със скорост v, се взриви на две части. Скоростта на един от фрагментите с маса m1 се увеличи в посоката на движение до стойността v1. Определете скоростта на втория фрагмент. 1. Обект на движение (граната): 2. Обектът е свободна система, връзки и реакциите им отсъстват. 3. Добавете активни сили: 4. Запишете теоремата за промяната на импулса: Проектирайте по оста: β Разделете променливите и интегрирайте: Десният интеграл е практически нула, тъй като време на експлозия t

22 слайд
Лекция 7 (продължение 7.3) 20 Ъгловият импулс на точка или ъгловият импулс на движение спрямо определен център е мярка за механично движение, определено от вектор, равен на векторното произведение на радиус вектора на материална точка от вектора на неговия импулс: Кинетичният момент на система от материални точки спрямо определен център е геометричен сумата от моментите на броя на движенията на всички материални точки спрямо същия център: В проекциите върху оста: В проекциите по оста: Теоремата за промяната на ъгловия импулс на системата - Разгледайте система от n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултантни Fke и Fki. Нека запишем основното уравнение на динамиката за всяка точка: или Сумирайте тези уравнения за всички точки: Заменете сбора от производни с производната на сумата: Изразът в скоби е моментът на момента на инерцията на системата. Следователно: Умножаваме всяко едно от равенствата векторно по радиус вектора отляво: Да видим дали знакът на производната може да бъде преместен извън векторното произведение: Така получаваме: Производната на вектора на ъгловия момент на системата спрямо някакъв център във времето е равно на главния момент на външните сили на системата спрямо същия център. При проекции върху координатните оси: Производната на ъгловия импулс на системата спрямо определена ос във времето е равна на главния момент на външните сили на системата спрямо същата ос.

23 слайд
Лекция 8 21 ■ Последици от теоремата за изменението на ъгловия импулс на системата (закони за запазване): 1. Ако във времевия интервал векторът на главния момент на външните сили на системата спрямо някакъв център е равен на нула, MOe = 0, тогава векторът на ъгловия импулс на системата спрямо същата централна константа, KO = const е законът за запазване на ъгловия импулс на системата). 2. Ако във времевия интервал основният момент на външните сили на системата спрямо оста x е равен на нула, Mxe = 0, то ъгловият импулс на системата спрямо оста x е постоянен, Kx = const. Подобни твърдения са верни за осите y и z. 2. Инерционен момент на твърдо тяло около оста: Моментът на инерция на материална точка около оста е равен на произведението на масата на точката на квадрата на разстоянието на точката до оста. Моментът на инерция на твърдо тяло около ос е равен на сумата от произведенията на масата на всяка точка на квадрата на разстоянието на тази точка до оста. ■ Елементи на теорията на инерционните моменти – Когато твърдо тяло се върти, мярката за инерция (съпротивление на промяна в движението) е моментът на инерция спрямо оста на въртене. Нека разгледаме основните понятия за дефиниция и методите за изчисляване на инерционните моменти. 1. Инерционен момент на материална точка около оста: При преминаване от дискретна малка маса към безкрайно малка маса на точка, границата на такава сума се определя от интеграла: аксиалния момент на инерция на твърдо тяло . В допълнение към аксиалния момент на инерция на твърдо тяло, има и други видове инерционни моменти: центробежният инерционен момент на твърдо тяло. полярен момент на инерция на твърдо тяло. 3. Теорема за инерционните моменти на твърдо тяло около успоредни оси - формулата за преход към успоредни оси: Инерционен момент около оригиналната ос Статични инерционни моменти около оригиналните оси Маса на тялото Разстояние между осите z1 и z2 Така: Ако оста z1 минава през центъра на масата, тогава статичните моменти са равни на нула:

24 слайд
Лекция 8 (продължение 8.2) 22 Инерционен момент на хомогенен прът с постоянно напречно сечение около оста: xz L Нека изберем елементарния обем dV = Adx на разстояние x: x dx Елементарна маса: За изчисляване на инерционния момент около централната ос (минаваща през центъра на тежестта), достатъчно е да промените позицията на оста и да зададете границите на интегриране (-L / 2, L / 2). Тук ще демонстрираме формулата за прехода към успоредни оси: zС 5. Инерционният момент на хомогенен твърд цилиндър спрямо оста на симетрия: H dr r Нека изберем елементарния обем dV = 2πrdrH (тънък цилиндър с радиус r) : Елементарна маса: Тук използвахме формулата за обема на цилиндъра V = πR2H. За да се изчисли инерционният момент на кух (дебел) цилиндър, е достатъчно да се зададат границите на интегриране от R1 до R2 (R2> R1): 6. Инерционен момент на тънък цилиндър около оста на симетрия (t

25 слайд
Лекция 8 (продължение 8.3) 23 ■ Диференциалното уравнение на въртене на твърдо тяло около ос: Нека напишем теорема за промяната в ъгловия импулс на твърдо тяло, въртящо се около фиксирана ос: Кинетичният момент на въртящо се твърдо тяло тялото е: Моментът на външните сили около оста на въртене е равен на въртящия момент (реакциите и силата на гравитацията не създават моменти): Заменете ъгловия импулс и въртящия момент в теоремата Пример: Двама души с еднакво тегло G1 = G2 висят на въже, хвърлено върху твърд блок с тегло G3 = G1 / 4. В един момент един от тях започна да се изкачва по въжето с относителна скорост u. Определете скоростта на повдигане на всеки от хората. 1. Избираме обекта на движение (блок с хора): 2. Изхвърляме връзките (поддържащото устройство на блока): 3. Заменяме връзката с реакции (лагер): 4. Добавяме активни сили (гравитация) : 5. Записваме теоремата за изменението на кинетичния момент на системата по отношение на осите на въртене на блока: R Тъй като моментът на външните сили е равен на нула, ъгловият импулс трябва да остане постоянен: При начален момент на времето t = 0, имаше равновесие и Kz0 = 0. След началото на движението на един човек спрямо въжето, цялата система започна да се движи, но системата с ъглов момент трябва да остане равна на нула: Kz = 0. Кинетичният момент на системата е сумата от кинетичните моменти както на хората, така и на блока: Тук v2 е скоростта на втория човек, равна на скоростта на кабела, Пример: Определете периода на малки свободни трептения на хомогенен прът с маса M и дължина l, окачен от единия край към фиксираната ос на въртене. Или: За малки трептения sinφ φ: Период на трептене: Инерционен момент:

26 слайд
Лекция 8 (продължение 8.4 - допълнителен материал) 24 ■ Елементарна теория на жироскопа: Жироскопът е твърдо тяло, въртящо се около ос на материална симетрия, една от точките на която е неподвижна. Свободен жироскоп - фиксиран така, че центърът на масата му остава неподвижен, а оста на въртене минава през центъра на масата и може да заема произволно положение в пространството, т.е. оста на въртене променя позицията си като оста на собственото си въртене на тялото по време на сферично движение. Основното предположение на приблизителната (елементарна) теория на жироскопа е, че векторът на ъгловия момент (ъгловия момент) на ротора се приема, че е насочен по собствената му ос на въртене. По този начин, въпреки факта, че в общия случай роторът участва в три завъртания, се взема предвид само ъгловата скорост на собственото му въртене ω = dφ / dt. Причината за това е, че в съвременната технология роторът на жироскопа се върти с ъглова скорост от порядъка на 5000-8000 rad/s (около 50 000-80000 rpm), докато другите две ъглови скорости, свързани с прецесията и нутацията на неговата собствена ос на въртене десетки хиляди пъти по-малка от тази скорост. Основното свойство на свободния жироскоп е, че оста на ротора поддържа постоянна посока в пространството по отношение на инерционната (звездна) референтна система (демонстрирана от махалото на Фуко, което поддържа равнината на люлеене непроменена по отношение на звездите, 1852 г.). Това следва от закона за запазване на ъгловия импулс спрямо центъра на масата на ротора, при условие че се пренебрегва триенето в лагерите на осите на окачването на ротора, външната и вътрешната рамка: Силово действие върху оста на свободен жироскоп. В случай на действие на сила, приложена към оста на ротора, моментът на външните сили спрямо центъра на масата не е равен на нула: сила и по посока на вектора на момента на тази сила, т.е. ще се върти не около оста x (вътрешно окачване), а около оста y (външно окачване). Когато силата спре да действа, оста на ротора ще остане в непроменена позиция, съответстваща на последния момент на действието на силата, т.к. от този момент във времето моментът на външните сили отново става равен на нула. В случай на краткотрайно действие на сила (удар) оста на жироскопа практически не променя позицията си. По този начин бързото въртене на ротора придава на жироскопа способността да противодейства на произволни влияния, склонни да променят положението на оста на въртене на ротора, и при постоянно действие на силата поддържа позицията на равнината, перпендикулярна на действащата сила в която лежи оста на ротора. Тези свойства се използват при работата на инерционните навигационни системи.
Преглед:тази статия е прочетена 32852 пъти
Pdf Изберете език ... Руски Украински Английски
Кратък преглед
Целият материал е изтеглен по-горе, като предварително сте избрали езика
- Статика
- Основни понятия за статиката
- Видове сили
- Аксиоми на статиката
- Връзките и техните реакции
- Система от сближаващи се сили
- Методи за определяне на резултантната система от сближаващи се сили
- Условия на равновесие за система от сближаващи се сили
- Момент на сила спрямо центъра като вектор
- Алгебрична величина на момента на сила
- Свойствата на момента на сила около центъра (точката)
- Теорията на двойките сили
- Събиране на две успоредни сили, насочени в една посока
- Събиране на две успоредни сили, насочени в противоположни посоки
- Двойки сили
- Теореми за двойка сили
- Условия на равновесие за система от двойки сили
- Рамото на лоста
- Произволна плоска система от сили
- Случаи на свеждане на плоска система от сили до по-проста форма
- Условия на аналитично равновесие
- Център на паралелните сили. Центърът на тежестта
- Център на паралелните сили
- Центърът на тежестта на твърдо тяло и неговите координати
- Център на тежестта на обема, равнината и правата
- Методи за определяне положението на центъра на тежестта
- Основи на изчисленията на силата
- Задачи и методи за якост на материалите
- Класификация на товарите
- Класификация на конструктивните елементи
- Деформации на пръта
- Основни хипотези и принципи
- Вътрешни сили. Метод на сечение
- Волтаж
- Разтягане и притискане
- Механични характеристики на материала
- Допустими напрежения
- Твърдост на материалите
- Графики на надлъжни сили и напрежения
- Shift
- Геометрични характеристики на сечения
- Усукване
- Огъване
- Ограничения на диференциално огъване
- Якост на огъване
- Нормални напрежения. Изчисляване на силата
- Напрежения при огъване на срязване
- Скованост при огъване
- Елементи от общата теория на напрегнатото състояние
- Теории за силата
- Торсионно огъване
- Кинематика
- Точкова кинематика
- Точкова траектория
- Методи за определяне на движението на точката
- Точкова скорост
- Точково ускорение
- Кинематика на твърдо тяло
- Транслационното движение на твърдо тяло
- Ротационно движение на твърдо тяло
- Кинематика на предавката
- Равнопаралелно движение на твърдо тяло
- Сложно движение на точки
- Точкова кинематика
- Динамика
- Основни закони на динамиката
- Точкова динамика
- Диференциални уравнения на свободна материална точка
- Два проблема на точковата динамика
- Динамика на твърдото тяло
- Класификация на силите, действащи върху механична система
- Диференциални уравнения на движение на механична система
- Общи теореми на динамиката
- Теорема за движението на центъра на масата на механична система
- Теорема за промяна на импулса
- Теоремата за промяната на ъгловия импулс
- Теорема за промяната на кинетичната енергия
- Сили, действащи в машините
- Сили при зацепване на цилиндрична предавка
- Триене в механизми и машини
- Триене на плъзгане
- Триене при търкаляне
- Ефективност
- Машинни части
- Механична трансмисия
- Видове механични трансмисии
- Основни и производни параметри на механичните трансмисии
- Скоростна трансмисия
- Предавания на гъвкава връзка
- Валове
- Предназначение и класификация
- Проектно изчисление
- Проверете изчислението на валовете
- Лагери
- Плъзгащи лагери
- Търкалящи се лагери
- Свързване на машинните части
- Видове разглобяеми и единични връзки
- Връзки с ключ
- Механична трансмисия
- Стандартизиране на нормите, взаимозаменяемост
- Допуски и кацания
- Единна система за отклонения и кацания (ESDP)
- Толерантност и позиция на формата
Формат: pdf
Размер: 4MB
руски език
Пример за изчисляване на цилиндрична предавка
Пример за изчисляване на цилиндрична предавка. Извършен е изборът на материал, изчисляването на допустимите напрежения, изчисляването на контактна и якост на огъване.
Пример за решаване на проблема с огъването на греда
В примера са изградени диаграми на срязващи сили и моменти на огъване, намира се опасен участък и се избира I-образна греда. Задачата анализира изграждането на диаграми с помощта на диференциални зависимости, извършва се сравнителен анализ на различни напречни сечения на гредата.
Пример за решаване на проблема с усукването на вала
Задачата е да се провери здравината на стоманен вал за даден диаметър, материал и допустими напрежения. По време на решението се изобразяват диаграми на въртящи моменти, напрежения на срязване и ъгли на усукване. Собственото тегло на вала не се взема предвид.
Пример за решаване на проблема с напрежение-компресия на пръта
Задачата е да се провери якостта на стоманената пръчка при дадено допустимо напрежение. В хода на решението се начертават диаграми на надлъжни сили, нормални напрежения и премествания. Собственото тегло на щангата не се взема предвид.
Приложение на теоремата за запазване на кинетичната енергия
Пример за решаване на задача за прилагането на теоремата за запазване на кинетичната енергия на механична система
Определяне на скоростта и ускорението на точка според дадените уравнения на движение
Пример за решаване на задача за определяне на скоростта и ускорението на точка според дадените уравнения на движение
Определяне на скоростите и ускоренията на точките на твърдо тяло по време на плоскопаралелно движение
Пример за решаване на задачата за определяне на скоростите и ускоренията на точките на твърдо тяло по време на плоскопаралелно движение
Определяне на силите в прътите на плоска ферма
Пример за решаване на проблема за определяне на силите в прътите на плоска ферма по метода на Ритер и метода за рязане на възли