សមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ត្រូវបានផ្តល់ឱ្យ។ សមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍មួយ។

ប្រភេទការងារ៖ ៧

លក្ខខណ្ឌ

បន្ទាត់ត្រង់ y=3x+2 គឺតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=-12x^2+bx-10។ រក b ដែលបានផ្តល់ឱ្យថា abscissa នៃចំណុចតង់សង់គឺតិចជាងសូន្យ។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

អនុញ្ញាតឱ្យ x_0 ជា abscissa នៃចំណុចនៅលើក្រាហ្វនៃអនុគមន៍ y=-12x^2+bx-10 ដែលតង់ហ្សង់ទៅក្រាហ្វនេះឆ្លងកាត់។

តម្លៃនៃដេរីវេនៅចំនុច x_0 គឺស្មើនឹងជម្រាលនៃតង់សង់ ពោលគឺ y"(x_0)=-24x_0+b=3។ ម្យ៉ាងវិញទៀត ចំនុចនៃតង់សង់ជាកម្មសិទ្ធិក្នុងពេលដំណាលគ្នានៃក្រាហ្វនៃ អនុគមន៍ និងតង់សង់ នោះគឺ -12x_0^2+bx_0-10= 3x_0 + 2។ យើងទទួលបានប្រព័ន្ធសមីការ \begin(cases) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2។ \end(ករណី)

ការដោះស្រាយប្រព័ន្ធនេះ យើងទទួលបាន x_0^2=1 ដែលមានន័យថា x_0=-1 ឬ x_0=1។ យោងតាមលក្ខខណ្ឌ abscissa ចំនុចតង់សង់គឺតិចជាងសូន្យ ដូច្នេះ x_0=-1 បន្ទាប់មក b=3+24x_0=-21។

ចម្លើយ

ប្រភេទការងារ៖ ៧
ប្រធានបទ៖ អត្ថន័យធរណីមាត្រនៃនិស្សន្ទវត្ថុ។ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍

លក្ខខណ្ឌ

បន្ទាត់ត្រង់ y=-3x+4 គឺស្របទៅនឹងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=-x^2+5x-7 ។ ស្វែងរក abscissa នៃចំណុចតង់សង់។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

មេគុណមុំនៃបន្ទាត់ត្រង់ទៅក្រាហ្វនៃអនុគមន៍ y=-x^2+5x-7 នៅចំណុចបំពាន x_0 គឺស្មើនឹង y"(x_0)។ ប៉ុន្តែ y"=-2x+5 ដែលមានន័យថា y" (x_0)=-2x_0+5. មេគុណមុំនៃបន្ទាត់ y=-3x+4 ដែលបានបញ្ជាក់ក្នុងលក្ខខណ្ឌគឺស្មើនឹង -3។ បន្ទាត់ប៉ារ៉ាឡែលមានមេគុណជម្រាលដូចគ្នា។ ដូច្នេះហើយ យើងរកឃើញតម្លៃ x_0 ដូចនេះ =- 2x_0 +5=-3 ។

យើងទទួលបាន: x_0 = 4 ។

ចម្លើយ

ប្រភព៖ "គណិតវិទ្យា។ ការរៀបចំសម្រាប់ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2017 ។ កម្រិតប្រវត្តិរូប។" អេដ។ F. F. Lysenko, S. Yu. Kulabukhova ។

លក្ខខណ្ឌ

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

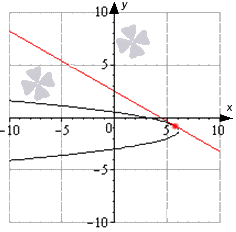
តាមរូប យើងកំណត់ថាតង់សង់ឆ្លងកាត់ចំណុច A(-6; 2) និង B(-1; 1) ។ ចូរយើងកំណត់ដោយ C(-6; 1) ចំនុចប្រសព្វនៃបន្ទាត់ x=-6 និង y=1 ហើយដោយ \alpha មុំ ABC (អ្នកអាចមើលឃើញក្នុងរូបថាវាស្រួច)។ បន្ទាប់មក បន្ទាត់ត្រង់ AB បង្កើតជាមុំ \pi -\alpha ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស Ox ដែលជា obtuse ។

ដូចដែលបានដឹងហើយថា tg(\pi -\alpha) នឹងជាតម្លៃនៃដេរីវេនៃអនុគមន៍ f(x) នៅចំណុច x_0។ បានកត់សម្គាល់ឃើញថា tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15។ពីទីនេះដោយប្រើរូបមន្តកាត់បន្ថយ យើងទទួលបាន៖ tg(\pi -\alpha) =-tg \alpha =-\frac15=-0.2 ។

ចម្លើយ

លក្ខខណ្ឌ

បន្ទាត់ត្រង់ y=-2x-4 គឺតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=16x^2+bx+12។ រក b ដែលបានផ្តល់ឱ្យថា abscissa នៃចំណុចតង់សង់គឺធំជាងសូន្យ។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

អនុញ្ញាតឱ្យ x_0 ជា abscissa នៃចំណុចនៅលើក្រាហ្វនៃអនុគមន៍ y=16x^2+bx+12 តាមរយៈនោះ

គឺតង់សង់ទៅនឹងក្រាហ្វនេះ។

តម្លៃនៃដេរីវេនៅចំនុច x_0 គឺស្មើនឹងចំណោទនៃតង់សង់ ពោលគឺ y"(x_0)=32x_0+b=-2។ ម្យ៉ាងវិញទៀតចំនុចនៃតង់សង់ជាកម្មសិទ្ធិក្នុងពេលដំណាលគ្នានៃក្រាហ្វនៃ អនុគមន៍ និងតង់សង់ នោះគឺ 16x_0^2+bx_0+12=- 2x_0-4 យើងទទួលបានប្រព័ន្ធសមីការ \begin(cases) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4។ \end(ករណី)

ការដោះស្រាយប្រព័ន្ធ យើងទទួលបាន x_0^2=1 ដែលមានន័យថា x_0=-1 ឬ x_0=1។ យោងតាមលក្ខខណ្ឌ abscissa ចំនុចតង់សង់គឺធំជាងសូន្យ ដូច្នេះ x_0=1 បន្ទាប់មក b=-2-32x_0=-34។

ចម្លើយ

លក្ខខណ្ឌ

តួលេខបង្ហាញក្រាហ្វនៃអនុគមន៍ y=f(x) ដែលកំណត់នៅលើចន្លោះពេល (-2; 8) ។ កំណត់ចំនួនចំនុចដែលតង់សង់ទៅក្រាហ្វនៃអនុគមន៍គឺស្របទៅនឹងបន្ទាត់ត្រង់ y=6 ។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

បន្ទាត់ត្រង់ y=6 គឺស្របទៅនឹងអ័ក្សអុក។ ដូច្នេះហើយ យើងរកឃើញចំណុចដែលតង់សង់ទៅក្រាហ្វនៃអនុគមន៍គឺស្របទៅនឹងអ័ក្សអុក។ នៅលើគំនូសតាងនេះ ចំណុចបែបនេះគឺជាចំណុចខ្លាំង (ពិន្ទុអតិបរមា ឬអប្បបរមា)។ ដូចដែលអ្នកអាចឃើញមាន 4 ចំណុចខ្លាំង។

ចម្លើយ

លក្ខខណ្ឌ

បន្ទាត់ y=4x-6 គឺស្របទៅនឹងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=x^2-4x+9។ ស្វែងរក abscissa នៃចំណុចតង់សង់។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

ជម្រាលតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=x^2-4x+9 នៅចំណុចបំពាន x_0 គឺស្មើនឹង y"(x_0)។ ប៉ុន្តែ y"=2x-4 ដែលមានន័យថា y"(x_0)= 2x_0-4. ជម្រាលនៃតង់សង់ y = 4x-7 ដែលបានបញ្ជាក់ក្នុងលក្ខខណ្ឌគឺស្មើនឹង 4. បន្ទាត់ប៉ារ៉ាឡែលមានមេគុណមុំដូចគ្នា ដូច្នេះហើយយើងរកឃើញតម្លៃនៃ x_0 ដូចនេះ 2x_0-4 = 4. យើង ទទួលបាន: x_0 = 4 ។

ចម្លើយ

លក្ខខណ្ឌ

តួលេខបង្ហាញក្រាហ្វនៃអនុគមន៍ y=f(x) និងតង់សង់ទៅវានៅចំណុចជាមួយ abscissa x_0 ។ ស្វែងរកតម្លៃនៃដេរីវេនៃអនុគមន៍ f(x) នៅចំណុច x_0។

បង្ហាញដំណោះស្រាយ

ដំណោះស្រាយ

តាមរូប យើងកំណត់ថាតង់សង់ឆ្លងកាត់ចំណុច A(1; 1) និង B(5; 4)។ អនុញ្ញាតឱ្យយើងកំណត់ដោយ C (5; 1) ចំណុចប្រសព្វនៃបន្ទាត់ x = 5 និង y = 1 និងដោយ \alpha មុំ BAC (អ្នកអាចមើលឃើញក្នុងរូបភាពថាវាស្រួច) ។ បន្ទាប់មក បន្ទាត់ត្រង់ AB បង្កើតជាមុំ \ អាល់ហ្វា ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្សអុក។

សមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍មួយ។

P. Romanov, T. Romanova,
Magnitogorsk,
តំបន់ Chelyabinsk

សមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍មួយ។

អត្ថបទនេះត្រូវបានបោះពុម្ពដោយមានការគាំទ្រពី ITAKA+ Hotel Complex។ នៅពេលស្នាក់នៅទីក្រុងអ្នកសាងសង់នាវា Severodvinsk អ្នកនឹងមិនជួបប្រទះបញ្ហាក្នុងការស្វែងរកលំនៅដ្ឋានបណ្តោះអាសន្នទេ។ នៅលើគេហទំព័រនៃអគារសណ្ឋាគារ “ITHAKA+” http://itakaplus.ru អ្នកអាចជួលអាផាតមិននៅក្នុងទីក្រុងបានយ៉ាងងាយស្រួល និងរហ័សក្នុងរយៈពេលណាមួយ ជាមួយនឹងការទូទាត់ប្រចាំថ្ងៃ។

នៅដំណាក់កាលនៃការអភិវឌ្ឍន៍ការអប់រំ ការងារសំខាន់មួយរបស់វាគឺការបង្កើតបុគ្គលិកលក្ខណៈនៃការគិតប្រកបដោយភាពច្នៃប្រឌិត។ សមត្ថភាពសម្រាប់ការច្នៃប្រឌិតរបស់សិស្សអាចត្រូវបានបង្កើតឡើងលុះត្រាតែពួកគេចូលរួមជាប្រព័ន្ធនៅក្នុងមូលដ្ឋាននៃសកម្មភាពស្រាវជ្រាវ។ មូលដ្ឋានគ្រឹះសម្រាប់សិស្សានុសិស្សក្នុងការប្រើប្រាស់ថាមពល សមត្ថភាព និងទេពកោសល្យច្នៃប្រឌិតរបស់ពួកគេត្រូវបានបង្កើតឡើងនូវចំណេះដឹង និងជំនាញពេញលេញ។ ក្នុងន័យនេះ បញ្ហានៃការបង្កើតប្រព័ន្ធនៃចំណេះដឹង និងជំនាញជាមូលដ្ឋានសម្រាប់ប្រធានបទនីមួយៗនៃវគ្គសិក្សាគណិតវិទ្យារបស់សាលាគឺមិនមានសារៈសំខាន់តិចតួចនោះទេ។ ក្នុងពេលជាមួយគ្នានេះ ជំនាញពេញលេញគួរតែជាគោលដៅដែលធ្វើមិនមែនសម្រាប់កិច្ចការបុគ្គលនោះទេ ប៉ុន្តែជាប្រព័ន្ធគិតគូរយ៉ាងយកចិត្តទុកដាក់ពីពួកគេ។ ក្នុងន័យទូលំទូលាយ ប្រព័ន្ធមួយត្រូវបានយល់ថាជាសំណុំនៃធាតុអន្តរកម្មអន្តរកម្មដែលមានភាពសុចរិត និងរចនាសម្ព័ន្ធស្ថិរភាព។

ចូរយើងពិចារណាបច្ចេកទេសសម្រាប់បង្រៀនសិស្សពីរបៀបសរសេរសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍មួយ។ ជាសំខាន់ បញ្ហាទាំងអស់នៃការស្វែងរកសមីការតង់ហ្សង់ធ្លាក់មកលើតម្រូវការក្នុងការជ្រើសរើសពីសំណុំ (បណ្តុំ, គ្រួសារ) នៃបន្ទាត់ដែលបំពេញតម្រូវការជាក់លាក់មួយ - ពួកគេគឺតង់សង់ទៅនឹងក្រាហ្វនៃមុខងារជាក់លាក់មួយ។ ក្នុងករណីនេះ សំណុំនៃបន្ទាត់ដែលការជ្រើសរើសត្រូវបានអនុវត្តអាចត្រូវបានបញ្ជាក់តាមពីរវិធី៖

ក) ចំណុចមួយនៅលើយន្តហោះ xOy (ខ្មៅដៃកណ្តាលនៃបន្ទាត់);
ខ) មេគុណមុំ (ធ្នឹមប៉ារ៉ាឡែលនៃបន្ទាត់ត្រង់) ។

ក្នុងន័យនេះ នៅពេលសិក្សាប្រធានបទ "តង់សង់ទៅនឹងក្រាហ្វនៃមុខងារ" ដើម្បីញែកធាតុនៃប្រព័ន្ធ យើងបានកំណត់បញ្ហាពីរប្រភេទ៖

1) បញ្ហានៅលើតង់សង់ដែលផ្តល់ដោយចំណុចដែលវាឆ្លងកាត់;
2) បញ្ហានៅលើតង់សង់ដែលផ្តល់ដោយជម្រាលរបស់វា។

ការបណ្តុះបណ្តាលក្នុងការដោះស្រាយបញ្ហាតង់សង់ត្រូវបានអនុវត្តដោយប្រើក្បួនដោះស្រាយដែលស្នើឡើងដោយ A.G. Mordkovich ។ ភាពខុសគ្នាជាមូលដ្ឋានរបស់វាពីអ្វីដែលស្គាល់រួចមកហើយគឺថា abscissa នៃចំណុចតង់សង់ត្រូវបានតំណាងដោយអក្សរ a (ជំនួសឱ្យ x0) ហើយដូច្នេះសមីការតង់សង់ត្រូវប្រើទម្រង់

y = f(a) + f "(a)(x − a)

(ប្រៀបធៀបជាមួយ y = f(x 0) + f "(x 0)(x – x 0))។ បច្ចេកទេសវិធីសាស្រ្តនេះ តាមគំនិតរបស់យើង អនុញ្ញាតឱ្យសិស្សយល់បានយ៉ាងរហ័ស និងងាយស្រួលពីកន្លែងដែលកូអរដោនេនៃចំណុចបច្ចុប្បន្នត្រូវបានសរសេរនៅក្នុង សមីការតង់ហ្សង់ទូទៅ និងកន្លែងដែលជាចំណុចទំនាក់ទំនង។

ក្បួនដោះស្រាយសម្រាប់បង្កើតសមីការតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = f(x)

1. កំណត់ abscissa នៃចំនុចតង់សង់ដោយអក្សរ a ។
2. រក f(a)។
3. រក f "(x) និង f "(a) ។
4. ជំនួសលេខដែលបានរកឃើញ a, f(a), f "(a) ទៅក្នុងសមីការតង់ហ្សង់ទូទៅ y = f(a) = f "(a)(x − a) ។

ក្បួនដោះស្រាយនេះអាចត្រូវបានចងក្រងដោយផ្អែកលើការកំណត់អត្តសញ្ញាណឯករាជ្យរបស់សិស្សនៃប្រតិបត្តិការ និងលំដាប់នៃការអនុវត្តរបស់ពួកគេ។

ការអនុវត្តបានបង្ហាញថាដំណោះស្រាយបន្តបន្ទាប់គ្នានៃបញ្ហាសំខាន់ៗនីមួយៗដោយប្រើក្បួនដោះស្រាយអនុញ្ញាតឱ្យអ្នកអភិវឌ្ឍជំនាញនៃការសរសេរសមីការនៃតង់សង់ទៅក្រាហ្វនៃមុខងារជាដំណាក់កាល ហើយជំហាននៃក្បួនដោះស្រាយបម្រើជាចំណុចយោងសម្រាប់សកម្មភាព។ . វិធីសាស្រ្តនេះត្រូវគ្នាទៅនឹងទ្រឹស្តីនៃការបង្កើតបន្តិចម្តងៗនៃសកម្មភាពផ្លូវចិត្តដែលបង្កើតឡើងដោយ P.Ya ។ Galperin និង N.F. តាលីស៊ីណា។

នៅក្នុងប្រភេទទីមួយ កិច្ចការសំខាន់ពីរត្រូវបានកំណត់អត្តសញ្ញាណ៖

តង់សង់ឆ្លងកាត់ចំណុចមួយនៅលើខ្សែកោង (បញ្ហា 1);
តង់សង់ឆ្លងកាត់ចំណុចដែលមិនស្ថិតនៅលើខ្សែកោង (បញ្ហាទី 2) ។

កិច្ចការ 1. សរសេរសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ នៅចំណុច M (3; - 2) ។

ដំណោះស្រាយ។ ចំណុច M (3; – 2) គឺជាចំណុចតង់សង់ចាប់តាំងពី

1. a = 3 – abscissa នៃចំណុចតង់សង់។
2. f(3) = − 2 ។
3. f "(x) = x 2 − 4, f "(3) = 5 ។
y = – 2 + 5(x – 3), y = 5x – 17 – សមីការតង់សង់។

បញ្ហា 2. សរសេរសមីការនៃតង់សង់ទាំងអស់ទៅក្រាហ្វនៃអនុគមន៍ y = – x 2 – 4x + 2 ឆ្លងកាត់ចំនុច M(– 3; 6) ។

ដំណោះស្រាយ។ ចំណុច M(– 3; 6) មិនមែនជាចំណុចតង់សង់ទេ ចាប់តាំងពី f(– 3) 6 (រូបទី 2) ។

2. f(a) = – a 2 – 4a + 2 ។
3. f “(x) = – 2x – 4, f “(a) = – 2a – 4 ។
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – សមីការតង់សង់។

តង់សង់ឆ្លងកាត់ចំណុច M(– 3; 6) ដូច្នេះ កូអរដោនេរបស់វាបំពេញសមីការតង់សង់។

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = – 4, a 2 = – 2 ។

ប្រសិនបើ a = – 4 នោះសមីការតង់សង់គឺ y = 4x + 18 ។

ប្រសិនបើ a = – 2 នោះសមីការតង់សង់មានទម្រង់ y = 6 ។

នៅក្នុងប្រភេទទីពីរ កិច្ចការសំខាន់ៗនឹងមានដូចខាងក្រោម៖

តង់សង់គឺស្របទៅនឹងបន្ទាត់មួយចំនួន (បញ្ហាទី 3);
តង់សង់ឆ្លងកាត់នៅមុំជាក់លាក់មួយទៅបន្ទាត់ដែលបានផ្តល់ឱ្យ (បញ្ហាទី 4) ។

បញ្ហា 3. សរសេរសមីការនៃតង់សង់ទាំងអស់ទៅក្រាហ្វនៃអនុគមន៍ y = x 3 – 3x 2 + 3 ស្របនឹងបន្ទាត់ y = 9x + 1 ។

ដំណោះស្រាយ។

1. a – abscissa នៃចំនុចតង់សង់។
2. f(a) = a 3 − 3a 2 + 3 ។
3. f "(x) = 3x 2 − 6x, f "(a) = 3a 2 − 6a ។

ប៉ុន្តែម្យ៉ាងវិញទៀត f "(a) = 9 (លក្ខខណ្ឌ parallelism) មានន័យថាយើងត្រូវដោះស្រាយសមីការ 3a 2 – 6a = 9 ។ ឫសរបស់វាគឺ a = – 1, a = 3 (រូបភាព 3 ។ )

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = − 1 + 9 (x + 1);

y = 9x + 8 – សមីការតង់សង់;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x − 3);

y = 9x – 24 – សមីការតង់សង់។

បញ្ហា 4. សរសេរសមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = 0.5x 2 – 3x + 1 ដោយឆ្លងកាត់នៅមុំ 45° ទៅបន្ទាត់ត្រង់ y = 0 (រូបភាព 4) ។

ដំណោះស្រាយ។ ពីលក្ខខណ្ឌ f "(a) = tan 45° យើងរកឃើញ a: a – 3 = 1^a = ៤.

1. a = 4 – abscissa នៃចំណុចតង់សង់។
2. f(4) = 8 − 12 + 1 = − 3 ។
3. f "(4) = 4 − 3 = 1 ។
4. y = − 3 + 1 (x − 4) ។

y = x − 7 – សមីការតង់សង់។

វាងាយស្រួលក្នុងការបង្ហាញថាដំណោះស្រាយចំពោះបញ្ហាផ្សេងទៀតគឺមកលើការដោះស្រាយបញ្ហាសំខាន់ៗមួយ ឬច្រើន។ ពិចារណាបញ្ហាពីរខាងក្រោមជាឧទាហរណ៍។

1. សរសេរសមីការនៃតង់សង់ទៅប៉ារ៉ាបូឡា y = 2x 2 – 5x – 2 ប្រសិនបើតង់សង់ប្រសព្វគ្នានៅមុំខាងស្តាំ ហើយមួយក្នុងចំណោមពួកវាប៉ះប៉ារ៉ាបូឡានៅចំណុចជាមួយ abscissa 3 (រូបភាព 5) ។

ដំណោះស្រាយ។ ចាប់តាំងពី abscissa នៃចំណុចតង់សង់ត្រូវបានផ្តល់ឱ្យផ្នែកដំបូងនៃដំណោះស្រាយត្រូវបានកាត់បន្ថយទៅជាបញ្ហាសំខាន់ 1 ។

1. a = 3 – abscissa នៃចំនុចនៃ tangency នៃជ្រុងម្ខាងនៃមុំខាងស្តាំ។
2. f(3) = 1.
3. f "(x) = 4x − 5, f "(3) = 7 ។
4. y = 1 + 7(x – 3), y = 7x – 20 – សមីការនៃតង់សង់ទីមួយ។

អនុញ្ញាតឱ្យ ក - មុំទំនោរនៃតង់សង់ទីមួយ។ ដោយសារតង់សង់គឺកាត់កែង នោះគឺជាមុំនៃទំនោរនៃតង់សង់ទីពីរ។ ពីសមីការ y = 7x – 20 នៃតង់សង់ទីមួយ យើងមាន tg a=7. ចូររក

នេះមានន័យថាជម្រាលនៃតង់សង់ទីពីរគឺស្មើនឹង .

ដំណោះស្រាយបន្ថែមទៀតចុះមកដល់កិច្ចការសំខាន់ ៣.

អនុញ្ញាតឱ្យ B(c; f(c)) ជាចំណុចនៃភាពតានតឹងនៃបន្ទាត់ទីពីរ បន្ទាប់មក

1. - abscissa នៃចំណុចទីពីរនៃ tangency ។
2.
3.
4.
- សមីការនៃតង់សង់ទីពីរ។

ចំណាំ។ មេគុណមុំនៃតង់សង់អាចត្រូវបានរកឃើញកាន់តែងាយស្រួលប្រសិនបើសិស្សដឹងពីសមាមាត្រនៃមេគុណនៃបន្ទាត់កាត់កែង k 1 k 2 = – 1 ។

2. សរសេរសមីការនៃតង់សង់ទូទៅទាំងអស់ទៅក្រាហ្វនៃអនុគមន៍

ដំណោះស្រាយ។ ភារកិច្ចគឺចុះមកដើម្បីស្វែងរក abscissa នៃចំណុចតង់សង់នៃតង់សង់ទូទៅ នោះគឺការដោះស្រាយបញ្ហាគន្លឹះ 1 ក្នុងទម្រង់ទូទៅ រៀបចំប្រព័ន្ធនៃសមីការហើយបន្ទាប់មកដោះស្រាយវា (រូបភាព 6) ។

1. ចូរឱ្យ a ជា abscissa នៃចំនុចតង់សង់ដែលស្ថិតនៅលើក្រាហ្វនៃអនុគមន៍ y = x 2 + x + 1 ។
2. f(a) = a 2 + a + 1 ។
3. f “(a) = 2a + 1 ។
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 ។

1. សូមអោយ c ជា abscissa នៃចំនុចតង់សង់ដែលស្ថិតនៅលើក្រាហ្វនៃអនុគមន៍
2.
3. f “(c) = គ.
4.

ចាប់តាំងពីតង់សង់ជាទូទៅ

ដូច្នេះ y = x + 1 និង y = – 3x – 3 គឺជាតង់សង់ទូទៅ។

គោលដៅសំខាន់នៃកិច្ចការដែលបានពិចារណាគឺរៀបចំសិស្សឱ្យស្គាល់ដោយឯករាជ្យនូវប្រភេទនៃបញ្ហាគន្លឹះ នៅពេលដោះស្រាយបញ្ហាស្មុគស្មាញបន្ថែមទៀត ដែលទាមទារជំនាញស្រាវជ្រាវជាក់លាក់ (សមត្ថភាពក្នុងការវិភាគ ប្រៀបធៀប ទូទៅ ដាក់ចេញនូវសម្មតិកម្ម។ល។)។ កិច្ចការទាំងនេះរួមបញ្ចូលកិច្ចការណាមួយដែលកិច្ចការសំខាន់ត្រូវបានរួមបញ្ចូលជាធាតុផ្សំ។ ចូរយើងពិចារណាជាឧទាហរណ៍អំពីបញ្ហា (បញ្ច្រាសទៅបញ្ហាទី 1) នៃការស្វែងរកមុខងារពីក្រុមគ្រួសារនៃតង់សង់របស់វា។

3. សម្រាប់អ្វីដែល b និង c ជាបន្ទាត់ y = x និង y = – 2x តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = x 2 + bx + c?

ដំណោះស្រាយ។

សូមឱ្យ t ជា abscissa នៃចំណុចនៃ tangency នៃបន្ទាត់ត្រង់ y = x ជាមួយប៉ារ៉ាបូឡា y = x 2 + bx + c; p គឺជា abscissa នៃចំនុចនៃ tangency នៃបន្ទាត់ត្រង់ y = – 2x ជាមួយ parabola y = x 2 + bx + c ។ បន្ទាប់មកសមីការតង់សង់ y = x នឹងយកទម្រង់ y = (2t + b)x + c – t 2 ហើយសមីការតង់សង់ y = – 2x នឹងយកទម្រង់ y = (2p + b)x + c–p 2 .

ចូរយើងចងក្រង និងដោះស្រាយប្រព័ន្ធសមីការ

ចម្លើយ៖

បញ្ហាដែលត្រូវដោះស្រាយដោយឯករាជ្យ

1. សរសេរសមីការនៃតង់សង់ដែលទាញទៅក្រាហ្វនៃអនុគមន៍ y = 2x 2 – 4x + 3 នៅចំនុចប្រសព្វនៃក្រាហ្វដែលមានបន្ទាត់ y = x + 3 ។

ចម្លើយ៖ y = – 4x + 3, y = 6x – 9.5 ។

2. សម្រាប់តម្លៃនៃ a តើតង់សង់ដែលទាញទៅក្រាហ្វនៃអនុគមន៍ y = x 2 – ax នៅចំណុចនៃក្រាហ្វដែលមាន abscissa x 0 = 1 ឆ្លងកាត់ចំណុច M(2; 3)?

ចម្លើយ៖ a = 0.5 ។

3. សម្រាប់តម្លៃ p តើបន្ទាត់ត្រង់ y = px – 5 ប៉ះខ្សែកោង y = 3x 2 – 4x – 2?

ចម្លើយ៖ ទំ ១ = – ១០, ទំ ២ = ២ ។

4. ស្វែងរកចំណុចទូទៅទាំងអស់នៃក្រាហ្វនៃអនុគមន៍ y = 3x – x 3 និងតង់សង់ដែលទាញទៅក្រាហ្វនេះតាមចំនុច P(0; 16)។

ចម្លើយ៖ A(2;–2), B(–4; 52)។

5. រកចម្ងាយខ្លីបំផុតរវាងប៉ារ៉ាបូឡា y = x 2 + 6x + 10 និងបន្ទាត់ត្រង់

ចម្លើយ៖

6. នៅលើខ្សែកោង y = x 2 – x + 1 រកចំណុចដែលតង់សង់ទៅក្រាហ្វគឺស្របទៅនឹងបន្ទាត់ត្រង់ y – 3x + 1 = 0 ។

ចម្លើយ៖ M(2; 3) ។

7. សរសេរសមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = x 2 + 2x – | 4x | ដែលប៉ះវានៅចំណុចពីរ។ ធ្វើគំនូរ។

ចម្លើយ៖ y = 2x − 4 ។

8. បង្ហាញថាបន្ទាត់ y = 2x − 1 មិនប្រសព្វខ្សែកោង y = x 4 + 3x 2 + 2x ។ ស្វែងរកចម្ងាយរវាងចំណុចជិតបំផុតរបស់ពួកគេ។

ចម្លើយ៖

9. នៅលើប៉ារ៉ាបូឡា y = x 2 ពិន្ទុពីរត្រូវបានយកជាមួយ abscissas x 1 = 1, x 2 = 3 ។ សេកង់មួយត្រូវបានទាញតាមចំនុចទាំងនេះ។ ត្រង់ចំណុចណានៃប៉ារ៉ាបូឡា តង់សង់ទៅវាស្របនឹងសេកុង? សរសេរសមីការលេខ និងតង់សង់។

ចម្លើយ៖ y = 4x – 3 – secant equation; y = 4x – 4 – សមីការតង់សង់។

10. រកមុំ q រវាងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = x 3 – 4x 2 + 3x + 1 គូរនៅចំនុចដោយ abscissas 0 និង 1 ។

ចម្លើយ៖ q = ៤៥°។

11. តើតង់សង់ទៅក្រាហ្វនៃអនុគមន៍បង្កើតមុំ 135° ជាមួយនឹងអ័ក្សអុកនៅចំនុចណា?

ចម្លើយ៖ A(0; – 1), B(4; 3)។

12. នៅចំណុច A(1; 8) ដល់ខ្សែកោង តង់សង់មួយត្រូវបានគូរ។ ស្វែងរកប្រវែងនៃផ្នែកតង់សង់រវាងអ័ក្សកូអរដោនេ។

ចម្លើយ៖

13. សរសេរសមីការនៃតង់សង់ទូទៅទាំងអស់ទៅក្រាហ្វនៃអនុគមន៍ y = x 2 – x + 1 និង y = 2x 2 – x + 0.5 ។

ចម្លើយ៖ y = – 3x និង y = x ។

14. រកចំងាយរវាងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ ស្របទៅនឹងអ័ក្ស x ។

ចម្លើយ៖

15. កំណត់នៅមុំណាដែលប៉ារ៉ាបូឡា y = x 2 + 2x − 8 កាត់អ័ក្ស x ។

ចម្លើយ៖ q 1 = arctan 6, q 2 = arctan (– 6) ។

16. ក្រាហ្វមុខងារ ស្វែងរកចំណុចទាំងអស់ តង់សង់នៅនីមួយៗនៃក្រាហ្វនេះប្រសព្វអ័ក្សពាក់កណ្តាលវិជ្ជមាននៃកូអរដោនេ ដោយកាត់ផ្តាច់ផ្នែកស្មើគ្នាពីពួកវា។

ចម្លើយ៖ ក(– ៣; ១១)។

17. បន្ទាត់ y = 2x + 7 និងប៉ារ៉ាបូឡា y = x 2 – 1 ប្រសព្វគ្នានៅចំនុច M និង N. រកចំនុច K ប្រសព្វនៃបន្ទាត់តង់សង់ទៅប៉ារ៉ាបូឡានៅចំនុច M និង N ។

ចម្លើយ៖ K(1;–9)។

18. សម្រាប់តម្លៃអ្វីនៃ b ជាបន្ទាត់ y = 9x + b តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = x 3 – 3x + 15?

ចម្លើយ៖ - ១; ៣១.

19. ចំពោះតម្លៃអ្វីនៃ k តើបន្ទាត់ត្រង់ y = kx – 10 មានចំណុចរួមតែមួយជាមួយក្រាហ្វនៃអនុគមន៍ y = 2x 2 + 3x – 2? ចំពោះតម្លៃដែលបានរកឃើញនៃ k កំណត់កូអរដោនេនៃចំណុច។

ចម្លើយ៖ k 1 = – 5, A(– 2; 0); k 2 = 11, B(2; 12) ។

20. សម្រាប់តម្លៃអ្វីនៃ b តើតង់សង់ដែលទាញទៅក្រាហ្វនៃអនុគមន៍ y = bx 3 – 2x 2 – 4 ត្រង់ចំនុចដែលមាន abscissa x 0 = 2 ឆ្លងកាត់ចំនុច M(1; 8)?

ចម្លើយ៖ ខ = − ៣ ។

21. ប៉ារ៉ាបូឡាដែលមានចំនុចកំពូលនៅលើអ័ក្សអុកប៉ះនឹងបន្ទាត់ដែលឆ្លងកាត់ចំនុច A(1; 2) និង B(2; 4) នៅចំនុច B. រកសមីការនៃប៉ារ៉ាបូឡា។

ចម្លើយ៖

22. តើតម្លៃនៃមេគុណ k តើប៉ារ៉ាបូឡា y = x 2 + kx + 1 ប៉ះអ័ក្សអុក?

ចម្លើយ៖ k = d ២.

23. រកមុំរវាងបន្ទាត់ត្រង់ y = x + 2 និងខ្សែកោង y = 2x 2 + 4x − 3 ។

29. រកចំងាយរវាងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ និងម៉ាស៊ីនភ្លើងដែលមានទិសដៅវិជ្ជមាននៃអ័ក្សអុកនៅមុំ 45°។

ចម្លើយ៖

30. រកទីតាំងនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡាទាំងអស់នៃទម្រង់ y = x 2 + ax + b តង់សង់ទៅបន្ទាត់ y = 4x − 1 ។

ចម្លើយ៖ បន្ទាត់ត្រង់ y = 4x + 3 ។

អក្សរសាស្ត្រ

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. ពិជគណិត និងការចាប់ផ្តើមនៃការវិភាគ៖ បញ្ហាចំនួន ៣៦០០ សម្រាប់សិស្សសាលា និងអ្នកដែលចូលសាកលវិទ្យាល័យ។ - M. , Bustard, ឆ្នាំ 1999 ។
2. Mordkovich A. សិក្ខាសាលាទីបួនសម្រាប់គ្រូបង្រៀនវ័យក្មេង។ ប្រធានបទ៖ កម្មវិធីដេរីវេ។ - M., "គណិតវិទ្យា", លេខ 21/94 ។
3. ការបង្កើតចំណេះដឹង និងជំនាញដោយផ្អែកលើទ្រឹស្តីនៃការបង្រួមបន្តិចម្តងៗនៃសកម្មភាពផ្លូវចិត្ត។ / Ed ។ ភី.យ៉ា. Galperina, N.F. តាលីស៊ីណា។ - M. , សាកលវិទ្យាល័យរដ្ឋម៉ូស្គូ, ឆ្នាំ 1968 ។

អត្ថបទផ្តល់នូវការពន្យល់លម្អិតនៃនិយមន័យ អត្ថន័យធរណីមាត្រនៃដេរីវេជាមួយសញ្ញាក្រាហ្វិក។ សមីការនៃបន្ទាត់តង់សង់នឹងត្រូវបានពិចារណាជាមួយឧទាហរណ៍ សមីការនៃតង់សង់ទៅខ្សែកោងលំដាប់ទី 2 នឹងត្រូវបានរកឃើញ។

Yandex.RTB R-A-339285-1 និយមន័យ 1

មុំទំនោរនៃបន្ទាត់ត្រង់ y = k x + b ត្រូវបានគេហៅថាមុំ α ដែលត្រូវបានវាស់ពីទិសដៅវិជ្ជមាននៃអ័ក្ស x ទៅបន្ទាត់ត្រង់ y = k x + b ក្នុងទិសដៅវិជ្ជមាន។

នៅក្នុងរូបភាព ទិស x ត្រូវបានចង្អុលបង្ហាញដោយព្រួញពណ៌បៃតង និងធ្នូពណ៌បៃតង និងមុំទំនោរដោយធ្នូក្រហម។ បន្ទាត់ពណ៌ខៀវសំដៅលើបន្ទាត់ត្រង់។

និយមន័យ ២

ចំណោទនៃបន្ទាត់ត្រង់ y = k x + b ត្រូវបានគេហៅថា មេគុណលេខ k ។

មេគុណមុំគឺស្មើនឹងតង់ហ្សង់នៃបន្ទាត់ត្រង់ និយាយម្យ៉ាងទៀត k = t g α ។

មុំទំនោរនៃបន្ទាត់ត្រង់គឺស្មើនឹង 0 លុះត្រាតែវាស្របគ្នាអំពី x ហើយជម្រាលគឺស្មើនឹងសូន្យ ពីព្រោះតង់សង់នៃសូន្យស្មើនឹង 0 ។ នេះមានន័យថាទម្រង់នៃសមីការនឹងជា y = b ។
ប្រសិនបើមុំទំនោរនៃបន្ទាត់ត្រង់ y = k x + b គឺស្រួច នោះលក្ខខណ្ឌ 0 គឺពេញចិត្ត< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 ហើយមានការកើនឡើងនៅក្នុងក្រាហ្វ។
ប្រសិនបើ α = π 2 នោះទីតាំងនៃបន្ទាត់គឺកាត់កែងទៅ x ។ សមភាពត្រូវបានបញ្ជាក់ដោយ x = c ជាមួយនឹងតម្លៃ c ជាចំនួនពិត។
ប្រសិនបើមុំទំនោរនៃបន្ទាត់ត្រង់ y = k x + b គឺ obtuse នោះវាត្រូវគ្នាទៅនឹងលក្ខខណ្ឌ π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

និយមន័យ ៣

សេកង់គឺជាបន្ទាត់ដែលឆ្លងកាត់ 2 ចំនុចនៃអនុគមន៍ f(x)។ ម្យ៉ាងវិញទៀត secant គឺជាបន្ទាត់ត្រង់មួយដែលត្រូវបានគូសតាមចំនុចពីរនៅលើក្រាហ្វនៃអនុគមន៍ដែលបានផ្តល់ឱ្យ។

តួរលេខបង្ហាញថា A B ជានិម្មិត ហើយ f (x) គឺជាខ្សែកោងខ្មៅ α គឺជាធ្នូក្រហម ដែលបង្ហាញពីមុំទំនោរនៃសេកង់។

នៅពេលដែលមេគុណមុំនៃបន្ទាត់ត្រង់ស្មើនឹងតង់ហ្សង់នៃមុំទំនោរ វាច្បាស់ណាស់ថាតង់សង់នៃត្រីកោណខាងស្តាំ A B C អាចត្រូវបានរកឃើញដោយសមាមាត្រនៃជ្រុងទល់មុខទៅនឹងមួយនៅជាប់គ្នា។

និយមន័យ ៤

យើងទទួលបានរូបមន្តសម្រាប់ស្វែងរកភាគនៃទម្រង់៖

k = t g α = B C A C = f (x B) - f x A x B - x A ដែល abscissas នៃចំនុច A និង B ជាតម្លៃ x A, x B, និង f (x A), f ( x ខ) គឺជាមុខងារតម្លៃនៅចំណុចទាំងនេះ។

ជាក់ស្តែង មេគុណមុំនៃសេកានត្រូវបានកំណត់ដោយប្រើសមភាព k = f (x B) - f (x A) x B - x A ឬ k = f (x A) - f (x B) x A - x B ហើយសមីការត្រូវតែសរសេរជា y = f (x B) - f (x A) x B - x A x - x A + f (x A) ឬ
y = f (x A) - f (x B) x A - x B x − x B + f (x B) ។

សេកចែកក្រាហ្វដោយមើលឃើញជា 3 ផ្នែក៖ នៅខាងឆ្វេងនៃចំណុច A ពី A ដល់ B ទៅខាងស្តាំនៃ B ។ រូបខាងក្រោមបង្ហាញថាមាន 3 សេណានដែលត្រូវបានចាត់ទុកថាស្របគ្នា ពោលគឺពួកវាត្រូវបានកំណត់ដោយប្រើ សមីការស្រដៀងគ្នា។

តាមនិយមន័យ វាច្បាស់ណាស់ថាបន្ទាត់ត្រង់ និងផ្នែករបស់វានៅក្នុងករណីនេះស្របគ្នា។

សេកានអាចប្រសព្វក្រាហ្វនៃអនុគមន៍ដែលបានផ្តល់ឱ្យច្រើនដង។ ប្រសិនបើមានសមីការនៃទម្រង់ y = 0 សម្រាប់ secant នោះចំនួនចំនុចប្រសព្វជាមួយ sinusoid គឺគ្មានកំណត់។

និយមន័យ ៥

តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f (x) នៅចំណុច x 0 ; f (x 0) គឺជាបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចដែលបានផ្តល់ឱ្យ x 0; f (x 0) ដោយមានវត្តមានផ្នែកដែលមានតម្លៃ x ជាច្រើននៅជិត x 0 ។

ឧទាហរណ៍ ១

ចូរយើងពិនិត្យមើលឱ្យកាន់តែដិតដល់នូវឧទាហរណ៍ខាងក្រោម។ បន្ទាប់មកវាច្បាស់ណាស់ថាបន្ទាត់ដែលបានកំណត់ដោយអនុគមន៍ y = x + 1 ត្រូវបានចាត់ទុកថាតង់សង់ទៅ y = 2 x នៅចំណុចដែលមានកូអរដោនេ (1; 2) ។ សម្រាប់ភាពច្បាស់លាស់វាចាំបាច់ត្រូវពិចារណាក្រាហ្វដែលមានតម្លៃជិត (1; 2) ។ អនុគមន៍ y = 2 x ត្រូវបានបង្ហាញជាពណ៌ខ្មៅ បន្ទាត់ពណ៌ខៀវគឺជាបន្ទាត់តង់សង់ ហើយចំនុចក្រហមគឺជាចំនុចប្រសព្វ។

ជាក់ស្តែង y = 2 x បញ្ចូលគ្នាជាមួយបន្ទាត់ y = x + 1 ។

ដើម្បីកំណត់តង់សង់ យើងគួរពិចារណាអំពីឥរិយាបទនៃតង់សង់ A B ខណៈដែលចំណុច B ចូលទៅជិតចំណុច A គ្មានកំណត់។ ដើម្បីឱ្យច្បាស់ យើងបង្ហាញគំនូរ។

secant A B ដែលបង្ហាញដោយបន្ទាត់ពណ៌ខៀវ មានទំនោរទៅទីតាំងនៃតង់សង់ខ្លួនវា ហើយមុំទំនោរនៃ secant α នឹងចាប់ផ្តើមមានទំនោរទៅមុំទំនោរនៃតង់សង់ខ្លួនវា α x ។

និយមន័យ ៦

តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = f (x) នៅចំណុច A ត្រូវបានចាត់ទុកថាជាទីតាំងកំណត់នៃសញ្ញា A B ដែល B មានទំនោរទៅ A នោះគឺ B → A ។

ឥឡូវនេះ ចូរយើងបន្តទៅពិចារណាអត្ថន័យធរណីមាត្រនៃដេរីវេនៃអនុគមន៍នៅចំណុចមួយ។

ចូរបន្តទៅការពិចារណាផ្នែក A B សម្រាប់អនុគមន៍ f (x) ដែល A និង B ដែលមានកូអរដោនេ x 0, f (x 0) និង x 0 + ∆ x, f (x 0 + ∆ x) ហើយ ∆ x គឺ តំណាងថាជាការកើនឡើងនៃអាគុយម៉ង់។ ឥឡូវនេះមុខងារនឹងយកទម្រង់ ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) ។ សម្រាប់ភាពច្បាស់លាស់ ចូរយើងផ្តល់ឧទាហរណ៍នៃគំនូរមួយ។

ពិចារណាពីលទ្ធផលត្រីកោណកែង A B C. យើងប្រើនិយមន័យនៃតង់សង់ដើម្បីដោះស្រាយ នោះគឺយើងទទួលបានទំនាក់ទំនង ∆ y ∆ x = t g α ។ ពីនិយមន័យនៃតង់សង់មួយ វាដូចខាងក្រោម lim ∆ x → 0 ∆ y ∆ x = t g α x ។ យោងតាមច្បាប់នៃដេរីវេទីវនៅចំណុចមួយ យើងមានថាដេរីវេ f (x) នៅចំណុច x 0 ត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ទៅនឹងការកើនឡើងនៃអាគុយម៉ង់ដែល ∆ x → 0 ។ បន្ទាប់មកយើងកំណត់វាជា f (x 0) = lim ∆ x → 0 ∆ y ∆ x ។

វាធ្វើតាម f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x ដែល k x ត្រូវបានតំណាងថាជាជម្រាលនៃតង់សង់។

នោះគឺយើងឃើញថា f '(x) អាចមាននៅចំណុច x 0 ហើយដូចជាតង់ហ្សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចនៃតង់សង់ស្មើនឹង x 0, f 0 (x 0) ដែលតម្លៃនៃ ជម្រាលនៃតង់សង់នៅចំណុចគឺស្មើនឹងដេរីវេនៅចំណុច x 0 ។ បន្ទាប់មកយើងទទួលបាន k x = f "(x 0) ។

អត្ថន័យធរណីមាត្រនៃដេរីវេនៃអនុគមន៍នៅចំណុចមួយគឺថាវាផ្តល់នូវគំនិតនៃអត្ថិភាពនៃតង់ហ្សង់ទៅក្រាហ្វនៅចំណុចដូចគ្នា។

ដើម្បីសរសេរសមីការនៃបន្ទាត់ត្រង់ណាមួយនៅលើយន្តហោះ ចាំបាច់ត្រូវមានមេគុណមុំជាមួយចំនុចដែលវាឆ្លងកាត់។ ការសម្គាល់របស់វាត្រូវបានយកជា x 0 នៅចំនុចប្រសព្វ។

សមីការតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = f (x) ត្រង់ចំនុច x 0, f 0 (x 0) យកទម្រង់ y = f "(x 0) x − x 0 + f (x 0) ។

នេះមានន័យថាតម្លៃចុងក្រោយនៃដេរីវេ f "(x 0) អាចកំណត់ទីតាំងនៃតង់សង់ នោះគឺ បញ្ឈរ បានផ្តល់ lim x → x 0 + 0 f "(x) = ∞ និង lim x → x 0 - 0 f "(x ) = ∞ ឬអវត្តមានទាំងអស់នៅក្រោមលក្ខខណ្ឌ lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) ។

ទីតាំងនៃតង់សង់អាស្រ័យទៅលើតម្លៃនៃមេគុណមុំរបស់វា k x = f "(x 0) នៅពេលប៉ារ៉ាឡែលទៅនឹងអ័ក្ស o x យើងទទួលបាននោះ k k = 0 នៅពេលប៉ារ៉ាឡែលទៅ o y − k x = ∞ និងទម្រង់នៃ សមីការតង់សង់ x = x 0 កើនឡើងជាមួយ k x > 0 ថយចុះជា k x< 0 .

ឧទាហរណ៍ ២

ចងក្រងសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 នៅចំណុចជាមួយកូអរដោនេ (1; 3) និងកំណត់មុំទំនោរ។

ដំណោះស្រាយ

តាមលក្ខខណ្ឌ យើងមានមុខងារត្រូវបានកំណត់សម្រាប់ចំនួនពិតទាំងអស់។ យើងរកឃើញថាចំនុចដែលមានកូអរដោណេដែលបានបញ្ជាក់ដោយលក្ខខណ្ឌ (1; 3) គឺជាចំណុចនៃតង់ស៊ីតេ បន្ទាប់មក x 0 = − 1, f (x 0) = − 3 ។

វាចាំបាច់ក្នុងការស្វែងរកដេរីវេនៅចំណុចជាមួយនឹងតម្លៃ - 1 ។ យើងទទួលបាននោះ។

y " = e x + 1 + x 3 3 − 6 − 3 3 x − 17 − 3 3 " = e x + 1 " + x 3 3 " - 6 − 3 3 x " - 17 − 3 3 " = e x + 1 + x 2 − 6 − 3 3 y " (x 0) = y " (- 1) = e − 1 + 1 + − 1 2 - 6 - 3 3 = 3 3

តម្លៃនៃ f '(x) នៅចំណុចនៃតង់សង់គឺជាជម្រាលនៃតង់សង់ដែលស្មើនឹងតង់ហ្សង់នៃជម្រាល។

បន្ទាប់មក k x = t g α x = y " (x 0) = 3 3

វាធ្វើតាមថា α x = a r c t g 3 3 = π 6

ចម្លើយ៖សមីការតង់ហ្សង់មានទម្រង់

y = f " (x 0) x − x 0 + f (x 0) y = 3 3 (x + 1) − 3 y = 3 3 x − 9 − 3 3

សម្រាប់ភាពច្បាស់លាស់ យើងផ្តល់ឧទាហរណ៍ក្នុងរូបភាពក្រាហ្វិក។

ពណ៌ខ្មៅត្រូវបានប្រើសម្រាប់ក្រាហ្វនៃមុខងារដើម ពណ៌ខៀវគឺជារូបភាពនៃតង់សង់ ហើយចំណុចក្រហមគឺជាចំណុចនៃភាពតានតឹង។ រូបនៅខាងស្តាំបង្ហាញទិដ្ឋភាពធំ។

ឧទាហរណ៍ ៣

កំណត់អត្ថិភាពនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ដែលបានផ្តល់ឱ្យ
y = 3 · x − 1 5 + 1 នៅចំណុចដែលមានកូអរដោណេ (1 ; 1) ។ សរសេរសមីការ និងកំណត់មុំទំនោរ។

ដំណោះស្រាយ

តាមលក្ខខណ្ឌ យើងមានថាដែននៃនិយមន័យនៃអនុគមន៍ដែលបានផ្តល់ឱ្យត្រូវបានចាត់ទុកថាជាសំណុំនៃចំនួនពិតទាំងអស់។

ចូរបន្តទៅការស្វែងរកដេរីវេ

y " = 3 x − 1 5 + 1 " = 3 1 5 (x − 1) 1 5 − 1 = 3 5 1 (x − 1) 4 5

ប្រសិនបើ x 0 = 1 នោះ f '(x) មិនត្រូវបានកំណត់ទេ ប៉ុន្តែដែនកំណត់ត្រូវបានសរសេរជា lim x → 1 + 0 3 5 1 (x − 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ និង lim x → 1 − 0 3 5 · 1 (x − 1) 4 5 = 3 5 · 1 (− 0) 4 5 = 3 5 · 1 + 0 = + ∞ មានន័យថា អត្ថិភាពតង់សង់បញ្ឈរនៅចំណុច (1; 1) ។

ចម្លើយ៖សមីការនឹងយកទម្រង់ x = 1 ដែលមុំទំនោរនឹងស្មើនឹង π 2 ។

ដើម្បីភាពច្បាស់លាស់ ចូរយើងពណ៌នាវាជាក្រាហ្វិក។

ឧទាហរណ៍ 4

រកចំណុចនៅលើក្រាហ្វនៃអនុគមន៍ y = 1 15 x + 2 3 − 4 5 x 2 − 16 5 x − 26 5 + 3 x + 2 ដែលជាកន្លែងដែល

មិនមានតង់សង់;
តង់សង់គឺស្របទៅនឹង x;
តង់សង់គឺស្របទៅនឹងបន្ទាត់ y = 8 5 x + 4 ។

ដំណោះស្រាយ

វាចាំបាច់ក្នុងការយកចិត្តទុកដាក់លើវិសាលភាពនៃនិយមន័យ។ តាមលក្ខខណ្ឌ យើងមានថាមុខងារត្រូវបានកំណត់លើសំណុំនៃចំនួនពិតទាំងអស់។ យើងពង្រីកម៉ូឌុល និងដោះស្រាយប្រព័ន្ធជាមួយចន្លោះពេល x ∈ - ∞ ; 2 និង [ - 2 ; + ∞) ។ យើងទទួលបាននោះ។

y = − 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ − ∞ ; − 2 1 15 x 3 − 6 x 2 + 9 x + 12 , x ∈ [ − 2 ; + ∞)

វាចាំបាច់ក្នុងការបែងចែកមុខងារ។ យើងមាននោះ។

y " = − 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ − ∞ ; − 2 1 15 x 3 − 6 x 2 + 9 x + 12 " , x ∈ [ − 2 ; + ∞ ) ⇔ y " = − 1 5 ( x 2 + 12 x + 35 ) , x ∈ − ∞ ; − 2 1 5 x 2 − 4 x + 3 , x ∈ [ − 2 ; + ∞)

នៅពេល x = − 2 នោះដេរីវេមិនមានទេ ដោយសារដែនកំណត់ម្ខាងមិនស្មើគ្នានៅចំណុចនោះ៖

lim x → − 2 − 0 y " (x) = lim x → − 2 − 0 − 1 5 (x 2 + 12 x + 35 = − 1 5 (− 2) 2 + 12 (− 2) + 35 = − 3 lim x → − 2 + 0 y " (x) = lim x → − 2 + 0 1 5 (x 2 − 4 x + 3) = 1 5 − 2 2 − 4 − 2 + 3 = 3

យើងគណនាតម្លៃនៃអនុគមន៍នៅចំណុច x = − 2 ដែលយើងទទួលបាននោះ។

y ( − 2 ) = 1 15 − 2 + 2 3 − 4 5 ( − 2 ) 2 − 16 5 ( − 2 ) − 26 5 + 3 − 2 + 2 = − 2 នោះគឺតង់សង់នៅចំណុច ( - 2; - 2) នឹងមិនមានទេ។
តង់សង់គឺស្របទៅនឹង x នៅពេលដែលជម្រាលគឺសូន្យ។ បន្ទាប់មក k x = t g α x = f "(x 0) នោះគឺជាការចាំបាច់ដើម្បីស្វែងរកតម្លៃនៃ x បែបនេះនៅពេលដែលដេរីវេនៃអនុគមន៍ប្រែវាទៅជាសូន្យ។ នោះគឺជាតម្លៃនៃ f ' (x) នឹងជាចំនុចនៃតង់សង់ ដែលតង់ហ្សង់គឺស្របទៅនឹង x ។

នៅពេល x ∈ − ∞ ; - 2 បន្ទាប់មក − 1 5 (x 2 + 12 x + 35) = 0 ហើយសម្រាប់ x ∈ ( − 2 ; + ∞ ) យើងទទួលបាន 1 5 ( x 2 − 4 x + 3 ) = 0 ។

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 − 4 35 = 144 − 140 = 4 x 1 = − 12 + 4 2 = − 5 ∈ − ∞ ; − 2 x 2 = − 12 − 4 2 = − 7 ∈ − ∞ ; − 2 1 5 (x 2 − 4 x + 3) = 0 D = 4 2 − 4 · 3 = 4 x 3 = 4 − 4 2 = 1 ∈ − 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ − 2 ; +∞

គណនាតម្លៃមុខងារដែលត្រូវគ្នា។

y 1 = y − 5 = 1 15 − 5 + 2 3 − 4 5 − 5 2 − 16 5 − 5 − 26 5 + 3 − 5 + 2 = 8 5 y 2 = y ( − 7 ) = 1 15 − 7 + 2 3 − 4 5 ( − 7 ) 2 − 16 5 − 7 − 26 5 + 3 − 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 − 4 5 1 2 − 16 5 1 − 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 − 4 5 3 2 − 16 5 3 − 26 5 + 3 3 + 2 = 4 3

ដូច្នេះ - 5; ៨ ៥,-៤; ៤ ៣, ១; ៨ ៥, ៣; 4 3 ត្រូវបានចាត់ទុកថាជាចំណុចដែលត្រូវការនៃក្រាហ្វមុខងារ។

សូមក្រឡេកមើលការបង្ហាញក្រាហ្វិកនៃដំណោះស្រាយ។

បន្ទាត់ខ្មៅគឺជាក្រាហ្វនៃមុខងារ ចំណុចក្រហមគឺជាចំណុចតង់ស៊ីតេ។

នៅពេលដែលបន្ទាត់ស្របគ្នា មេគុណមុំគឺស្មើគ្នា។ បន្ទាប់មកចាំបាច់ត្រូវស្វែងរកចំណុចនៅលើក្រាហ្វមុខងារដែលជម្រាលនឹងស្មើនឹងតម្លៃ 8 5 ។ ដើម្បីធ្វើដូចនេះអ្នកត្រូវដោះស្រាយសមីការនៃទម្រង់ y "(x) = 8 5. បន្ទាប់មកប្រសិនបើ x ∈ − ∞ ; - 2 យើងទទួលបាននោះ - 1 5 (x 2 + 12 x + 35) = 8 5 ហើយប្រសិនបើ x ∈ ( − 2 ; + ∞ ) នោះ 1 5 ( x 2 − 4 x + 3 ) = 8 5 ។

សមីការទីមួយមិនមានឫសគល់ទេ ដោយសារអ្នករើសអើងគឺតិចជាងសូន្យ។ ចូរយើងសរសេរចុះ

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 − 4 43 = − 28< 0

សមីការមួយទៀតមានឫសពិតពីរ

1 5 (x 2 − 4 x + 3) = 8 5 x 2 − 4 x − 5 = 0 D = 4 2 − 4 · (− 5) = 36 x 1 = 4 − 36 2 = − 1 ∈ − 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ − 2 ; +∞

ចូរបន្តទៅការស្វែងរកតម្លៃនៃមុខងារ។ យើងទទួលបាននោះ។

y 1 = y (- 1) = 1 15 − 1 + 2 3 − 4 5 ( − 1 ) 2 − 16 5 ( − 1 ) − 26 5 + 3 − 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

ពិន្ទុជាមួយតម្លៃ - 1; ៤ ១៥, ៥; 8 3 គឺជាចំនុចដែលតង់សង់ស្របនឹងបន្ទាត់ y = 8 5 x + 4 ។

ចម្លើយ៖បន្ទាត់ខ្មៅ - ក្រាហ្វនៃមុខងារ បន្ទាត់ក្រហម - ក្រាហ្វនៃ y = 8 5 x + 4 បន្ទាត់ពណ៌ខៀវ - តង់សង់នៅចំណុច - 1; ៤ ១៥, ៥; ៨ ៣.

វាអាចមានតង់ហ្សង់ចំនួនមិនកំណត់សម្រាប់អនុគមន៍ដែលបានផ្តល់ឱ្យ។

ឧទាហរណ៍ 5

សរសេរសមីការនៃតង់សង់ដែលមានទាំងអស់នៃអនុគមន៍ y = 3 cos 3 2 x − π 4 − 1 3 ដែលមានទីតាំងនៅកាត់កែងទៅនឹងបន្ទាត់ត្រង់ y = − 2 x + 1 2 ។

ដំណោះស្រាយ

ដើម្បីចងក្រងសមីការតង់សង់ វាចាំបាច់ក្នុងការស្វែងរកមេគុណ និងកូអរដោនេនៃចំណុចតង់សង់ដោយផ្អែកលើលក្ខខណ្ឌនៃការកាត់កែងនៃបន្ទាត់។ និយមន័យមានដូចខាងក្រោម៖ ផលគុណនៃមេគុណមុំដែលកាត់កែងទៅនឹងបន្ទាត់ត្រង់គឺស្មើនឹង − 1 ពោលគឺសរសេរជា k x · k ⊥ = − 1 ។ ពីលក្ខខណ្ឌយើងមានថាមេគុណមុំមានទីតាំងនៅកាត់កែងទៅនឹងបន្ទាត់ហើយស្មើនឹង k ⊥ = − 2 បន្ទាប់មក k x = − 1 k ⊥ = - 1 − 2 = 1 2 ។

ឥឡូវអ្នកត្រូវស្វែងរកកូអរដោនេនៃចំណុចប៉ះ។ អ្នកត្រូវស្វែងរក x ហើយបន្ទាប់មកតម្លៃរបស់វាសម្រាប់មុខងារដែលបានផ្តល់ឱ្យ។ ចំណាំថាពីអត្ថន័យធរណីមាត្រនៃដេរីវេនៅចំណុច
x 0 យើងទទួលបាននោះ k x = y” (x 0) ពីសមភាពនេះ យើងរកឃើញតម្លៃនៃ x សម្រាប់ចំណុចទំនាក់ទំនង។

យើងទទួលបាននោះ។

y " (x 0) = 3 cos 3 2 x 0 − π 4 − 1 3 " = 3 - sin 3 2 x 0 − π 4 3 2 x 0 − π 4 " = = − 3 sin 3 2 x 0 − π 4 3 2 = − 9 2 sin 3 2 x 0 − π 4 ⇒ k x = y " (x 0) ⇔ − 9 2 sin 3 2 x 0 − π 4 = 1 2 ⇒ sin 3 2 x 0 − π 4 = − 19

សមីការត្រីកោណមាត្រនេះនឹងត្រូវបានប្រើដើម្បីគណនាលំដាប់នៃចំណុចតង់សង់។

3 2 x 0 − π 4 = a r c sin - 1 9 + 2 πk ឬ 3 2 x 0 − π 4 = π − a r c sin - 1 9 + 2 πk

3 2 x 0 − π 4 = − a r c sin 1 9 + 2 πk ឬ 3 2 x 0 − π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 − a r c sin 1 9 + 2 πk ឬ x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z គឺជាសំណុំនៃចំនួនគត់។

x ចំណុចទំនាក់ទំនងត្រូវបានរកឃើញ។ ឥឡូវអ្នកត្រូវបន្តទៅការស្វែងរកតម្លៃនៃ y៖

y 0 = 3 cos 3 2 x 0 − π 4 − 1 ៣

y 0 = 3 1 − sin 2 3 2 x 0 − π 4 − 1 3 ឬ y 0 = 3 − 1 − sin 2 3 2 x 0 − π 4 − 1 3

y 0 = 3 1 − 1 9 2 − 1 3 ឬ y 0 = 3 − 1 − − 1 9 2 − 1 3

y 0 = 4 5 − 1 3 ឬ y 0 = − 4 5 + 1 3

ពីនេះយើងទទួលបាន 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 គឺជាចំនុចនៃ tangency ។

ចម្លើយ៖សមីការចាំបាច់នឹងត្រូវបានសរសេរជា

y = 1 2 x − 2 3 π 4 − a r c sin 1 9 + 2 πk + 4 5 − 1 3 , y = 1 2 x − 2 3 5 π 4 + a r c sin 1 9 + 2 πk − 4 5 + 1 3 , k ∈ Z

សម្រាប់ការតំណាងដែលមើលឃើញ សូមពិចារណាមុខងារ និងតង់សង់នៅលើបន្ទាត់កូអរដោនេ។

តួលេខបង្ហាញថាមុខងារមានទីតាំងនៅចន្លោះពេល [ - 10 ; 10] ដែលបន្ទាត់ខ្មៅជាក្រាហ្វនៃអនុគមន៍ បន្ទាត់ពណ៌ខៀវគឺជាតង់សង់ដែលមានទីតាំងនៅកាត់កែងទៅនឹងបន្ទាត់ដែលបានផ្តល់ឱ្យនៃទម្រង់ y = − 2 x + 1 2 ។ ចំណុចក្រហមគឺជាចំណុចប៉ះ។

សមីការ Canonical នៃខ្សែកោងលំដាប់ទី 2 មិនមែនជាមុខងារតម្លៃតែមួយទេ។ សមីការតង់សង់សម្រាប់ពួកវាត្រូវបានចងក្រងតាមគ្រោងការណ៍ដែលគេស្គាល់។

តង់សង់ទៅរង្វង់មួយ។

ដើម្បីកំណត់រង្វង់ដែលមានចំណុចកណ្តាល x c e n t e r ; y c e n t e r និង កាំ R អនុវត្តរូបមន្ត x − x c e n t e r 2 + y − y c e n t e r 2 = R 2 ។

សមភាពនេះអាចត្រូវបានសរសេរជាសហជីពនៃមុខងារពីរ៖

y = R 2 − x − x c e n t e r 2 + y c e n t e r y = − R 2 − x − x c e n t e r 2 + y c e n t e r

មុខងារទីមួយមានទីតាំងនៅផ្នែកខាងលើ និងទីពីរនៅខាងក្រោម ដូចបង្ហាញក្នុងរូប។

ដើម្បីចងក្រងសមីការនៃរង្វង់នៅចំណុច x 0; y 0 ដែលមានទីតាំងនៅផ្នែកខាងលើ ឬខាងក្រោម អ្នកគួរតែស្វែងរកសមីការនៃក្រាហ្វនៃមុខងារនៃទម្រង់ y = R 2 - x - x c e n t e r 2 + y c e n t e r ឬ y = - R 2 - x - x c e n t e r 2 + y c e n t e r នៅចំណុចដែលបានចង្អុលបង្ហាញ។

នៅពេលដែលនៅចំណុច x c e n t e r ; y c e n t e r + R និង x c e n t e r ; y c e n t e r - R តង់សង់អាចត្រូវបានផ្តល់ដោយសមីការ y = y c e n t e r + R និង y = y c e n t e r - R ហើយនៅចំណុច x c e n t e r + R ; y c e n t e r និង
x c e n t e r - R ; y c e n t e r នឹងស្របទៅនឹង o y បន្ទាប់មកយើងទទួលបានសមីការនៃទម្រង់ x = x c e n t e r + R និង x = x c e n t e r - R ។

តង់សង់ទៅពងក្រពើ

នៅពេលដែលពងក្រពើមានចំណុចកណ្តាល x c e n t e r ; y c e n t e r ជាមួយអ័ក្សពាក់កណ្តាល a និង b បន្ទាប់មកវាអាចត្រូវបានបញ្ជាក់ដោយប្រើសមីការ x − x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 ។

រាងពងក្រពើ និងរង្វង់អាចត្រូវបានបង្ហាញដោយការរួមបញ្ចូលគ្នានូវមុខងារពីរគឺរាងពងក្រពើខាងលើ និងខាងក្រោម។ បន្ទាប់មកយើងទទួលបានវា។

y = b a · a 2 − (x − x c e n t e r) 2 + y c e n t e r y = − b a · a 2 − (x − x c e n t e r) 2 + y c e n t e r

ប្រសិនបើតង់សង់ស្ថិតនៅចំនុចកំពូលនៃពងក្រពើ នោះពួកវាស្របគ្នាប្រហែល x ឬប្រហែល y ។ ខាងក្រោមសម្រាប់ភាពច្បាស់លាស់សូមពិចារណារូបភាព។

ឧទាហរណ៍ ៦

សរសេរសមីការនៃតង់សង់ទៅពងក្រពើ x − 3 2 4 + y − 5 2 25 = 1 នៅចំនុចដែលមានតម្លៃ x ស្មើនឹង x = 2 ។

ដំណោះស្រាយ

វាចាំបាច់ក្នុងការស្វែងរកចំណុចតង់សង់ដែលត្រូវគ្នានឹងតម្លៃ x = 2 ។ យើងជំនួសសមីការដែលមានស្រាប់នៃពងក្រពើ ហើយរកឃើញវា។

x − 3 2 4 x = 2 + y − 5 2 25 = 1 1 4 + y − 5 2 25 = 1 ⇒ y − 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

បន្ទាប់មក 2; 5 3 2 + 5 និង 2; - 5 3 2 + 5 គឺជាចំណុចតង់សង់ដែលជារបស់ពងក្រពើខាងលើ និងខាងក្រោម។

ចូរបន្តទៅការស្វែងរក និងដោះស្រាយសមីការនៃពងក្រពើដោយគោរពទៅ y ។ យើងទទួលបាននោះ។

x − 3 2 4 + y − 5 2 25 = 1 y − 5 2 25 = 1 − x − 3 2 4 ( y − 5 ) 2 = 25 1 − x − 3 2 4 y − 5 = ± 5 1 − x − 3 2 4 y = 5 ± 5 2 4 − x − 3 2

ជាក់ស្តែង ពងក្រពើពាក់កណ្តាលខាងលើត្រូវបានបញ្ជាក់ដោយប្រើមុខងារនៃទម្រង់ y = 5 + 5 2 4 − x − 3 2 និងពងក្រពើពាក់កណ្តាលខាងក្រោម y = 5 − 5 2 4 − x − 3 2 ។

ចូរយើងអនុវត្តក្បួនដោះស្រាយស្តង់ដារដើម្បីបង្កើតសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចមួយ។ ចូរយើងសរសេរថាសមីការសម្រាប់តង់សង់ទីមួយនៅចំណុច 2; 5 3 2 + 5 នឹងមើលទៅដូច

y " = 5 + 5 2 4 − x − 3 2 ” = 5 2 1 2 4 − (x − 3) 2 4 − (x − 3) 2” = = − 5 2 x − 3 4 − ( x − 3 ) ) 2 ⇒ y " (x 0) = y " (2) = − 5 2 2 - 3 4 - (2 − 3) 2 = 5 2 3 ⇒ y = y " (x 0) x − x 0 + y 0 ⇔ y = 5 2 3 (x − 2) + 5 3 2 + 5

យើងរកឃើញថាសមីការនៃតង់សង់ទីពីរជាមួយនឹងតម្លៃនៅចំណុច
2 ; - 5 3 2 + 5 យកទម្រង់

y” = 5 − 5 2 4 − (x − 3) 2” = − 5 2 1 2 4 − (x − 3) 2 4 − (x − 3) 2” = = 5 2 x − 3 4 − (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 − 3 4 - (2 − 3) 2 = − 5 2 3 ⇒ y = y " (x 0) x − x 0 + y 0 ⇔ y = − 5 2 3 (x − 2) − 5 3 2 + 5

តាមក្រាហ្វិក តង់សង់ត្រូវបានកំណត់ដូចខាងក្រោម៖

តង់សង់ទៅអ៊ីពែបូល។

នៅពេលដែលអ៊ីពែបូឡាមានមជ្ឈមណ្ឌលនៅ x c e n t e r ; y c e n t e r និង vertices x c e n t e r + α ; y c e n t e r និង x c e n t e r - α ; y c e n t e r , វិសមភាព x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 កើតឡើងប្រសិនបើមានចំនុចកំពូល x c e n t e r ; y c e n t e r + b និង x c e n t e r ; y c e n t e r - b បន្ទាប់មកត្រូវបានបញ្ជាក់ដោយប្រើវិសមភាព x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 ។

អ៊ីពែបូឡាអាចត្រូវបានតំណាងថាជាមុខងាររួមបញ្ចូលគ្នាពីរនៃទម្រង់

y = b a · ( x − x c e n t e r ) 2 − a 2 + y c e n t e r y = − b a · ( x − x c e n t e r ) 2 − a 2 + y c e n t e r ឬ y = b a · ( x − t 2 c e e ) r y = - b a · (x − x c e n t e r) 2 + a 2 + y c e n t e r

ក្នុងករណីទី 1 យើងមានតង់សង់គឺស្របទៅនឹង y ហើយនៅក្នុងទីពីរវាស្របទៅនឹង x ។

វាធ្វើតាមថា ដើម្បីស្វែងរកសមីការនៃតង់សង់ទៅអ៊ីពែបូឡា វាចាំបាច់ត្រូវរកឱ្យឃើញនូវមុខងារណាមួយដែលចំណុចតង់សង់ជាកម្មសិទ្ធិ។ ដើម្បីកំណត់នេះ វាចាំបាច់ក្នុងការជំនួសសមីការ និងពិនិត្យមើលអត្តសញ្ញាណ។

ឧទាហរណ៍ ៧

សរសេរសមីការសម្រាប់តង់សង់ទៅអ៊ីពែបូឡា x − 3 2 4 − y + 3 2 9 = 1 នៅចំនុចទី 7; - ៣ ៣ - ៣ .

ដំណោះស្រាយ

វាចាំបាច់ក្នុងការបំប្លែងកំណត់ត្រាដំណោះស្រាយសម្រាប់ការស្វែងរកអ៊ីពែបូឡាដោយប្រើមុខងារ 2 ។ យើងទទួលបាននោះ។

x − 3 2 4 − y + 3 2 9 = 1 ⇒ y + 3 2 9 = x − 3 2 4 − 1 ⇒ y + 3 2 = 9 x − 3 2 4 − 1 ⇒ y + 3 = 3 2 x − 3 2 − 4 និង y + 3 = − 3 2 x − 3 2 − 4 ⇒ y = 3 2 x − 3 2 − 4 − 3 y = − 3 2 x − 3 2 − 4 − 3

វាចាំបាច់ដើម្បីកំណត់មុខងារណាមួយដែលចំណុចដែលបានផ្តល់ឱ្យដែលមានកូអរដោនេ 7 ជាកម្មសិទ្ធិ។ - ៣ ៣ - ៣ .

ជាក់ស្តែង ដើម្បីពិនិត្យមើលមុខងារទីមួយ វាចាំបាច់ y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 បន្ទាប់មកចំនុចមិនមែនជារបស់ក្រាហ្វទេ ចាប់តាំងពីសមភាពមិនកាន់។

សម្រាប់អនុគមន៍ទីពីរ យើងមានថា y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 ដែលមានន័យថាចំនុចនោះជារបស់ក្រាហ្វដែលបានផ្តល់ឱ្យ។ ពីទីនេះអ្នកគួរស្វែងរកជម្រាល។

យើងទទួលបាននោះ។

y” = − 3 2 (x − 3) 2 − 4 − 3 “ = − 3 2 x − 3 (x − 3) 2 − 4 ⇒ k x = y” (x 0) = − 3 2 x 0 − 3 x 0 − 3 2 − 4 x 0 = 7 = − 3 2 7 − 3 7 − 3 2 − 4 = − 3

ចម្លើយ៖សមីការតង់សង់អាចត្រូវបានតំណាងជា

y = − 3 x − 7 − 3 3 − 3 = − 3 x + 4 3 − 3

វាត្រូវបានពិពណ៌នាយ៉ាងច្បាស់ដូចនេះ៖

តង់សង់ទៅប៉ារ៉ាបូឡា

ដើម្បីបង្កើតសមីការសម្រាប់តង់សង់ទៅប៉ារ៉ាបូឡា y = a x 2 + b x + c នៅចំណុច x 0, y (x 0) អ្នកត្រូវប្រើក្បួនដោះស្រាយស្តង់ដារ បន្ទាប់មកសមីការនឹងយកទម្រង់ y = y "(x 0) x − x 0 + y ( x 0)។តង់សង់បែបនេះនៅចំនុចកំពូលគឺស្របទៅនឹង x ។

អ្នកគួរតែកំណត់ parabola x = a y 2 + b y + c ជាការរួបរួមនៃអនុគមន៍ពីរ។ ដូច្នេះយើងត្រូវដោះស្រាយសមីការសម្រាប់ y ។ យើងទទួលបាននោះ។

x = a y 2 + b y + c ⇔ a y 2 + b y + c − x = 0 D = b 2 − 4 a (c − x) y = − b + b 2 − 4 a (c − x) 2 a y = − b − b 2 − 4 a (c − x) 2 ក

បង្ហាញជាក្រាហ្វិកដូចជា៖

ដើម្បីរកមើលថាតើចំនុច x 0, y (x 0) ជាកម្មសិទ្ធិរបស់មុខងារ ឬអត់ សូមបន្តដោយថ្នមៗតាមក្បួនដោះស្រាយស្តង់ដារ។ តង់សង់បែបនេះនឹងស្របទៅនឹង o y ដែលទាក់ទងទៅនឹងប៉ារ៉ាបូឡា។

ឧទាហរណ៍ ៨

សរសេរសមីការនៃតង់សង់ទៅក្រាហ្វ x − 2 y 2 – 5 y + 3 នៅពេលយើងមានមុំតង់សង់ 150 °។

ដំណោះស្រាយ

យើងចាប់ផ្តើមដំណោះស្រាយដោយតំណាងឱ្យប៉ារ៉ាបូឡាជាមុខងារពីរ។ យើងទទួលបាននោះ។

. ៤៩ − ៨ x − ៤

តម្លៃនៃជម្រាលគឺស្មើនឹងតម្លៃនៃដេរីវេនៅចំណុច x 0 នៃអនុគមន៍នេះ ហើយស្មើនឹងតង់ហ្សង់នៃមុំទំនោរ។

យើងទទួលបាន:

k x = y "(x 0) = t g α x = t g 150 ° = − 1 3

ពីទីនេះយើងកំណត់តម្លៃ x សម្រាប់ចំណុចទំនាក់ទំនង។

មុខងារទីមួយនឹងត្រូវបានសរសេរជា

y " = 5 + 49 − 8 x − 4 " = 1 49 − 8 x ⇒ y " (x 0) = 1 49 − 8 x 0 = − 1 3 ⇔ 49 − 8 x 0 = − 3

ជាក់ស្តែង មិនមានឫសគល់ពិតប្រាកដទេ ចាប់តាំងពីយើងទទួលបានតម្លៃអវិជ្ជមាន។ យើងសន្និដ្ឋានថាមិនមានតង់សង់ដែលមានមុំ 150° សម្រាប់មុខងារបែបនេះទេ។

មុខងារទីពីរនឹងត្រូវបានសរសេរជា

y " = 5 − 49 − 8 x − 4 " = − 1 49 − 8 x ⇒ y " (x 0) = − 1 49 − 8 x 0 = − 1 3 ⇔ 49 − 8 x 0 = − 3 x 0 = 23 4 ⇒ y (x 0) = 5 − 49 − 8 23 4 − 4 = − 5 + 3 4

យើងមានថាចំណុចនៃទំនាក់ទំនងគឺ 23 4 ; - ៥ + ៣ ៤ .

ចម្លើយ៖សមីការតង់ហ្សង់មានទម្រង់

y = − 1 3 x − 23 4 + − 5 + 3 ៤

ចូរពណ៌នាវាជាក្រាហ្វិកតាមវិធីនេះ៖

ប្រសិនបើអ្នកសម្គាល់ឃើញកំហុសនៅក្នុងអត្ថបទ សូមរំលេចវា ហើយចុច Ctrl+Enter

អនុញ្ញាតឱ្យអនុគមន៍ f ត្រូវបានផ្តល់ឱ្យ ដែលនៅចំណុចមួយចំនួន x 0 មានដេរីវេកំណត់ f (x 0) ។ បន្ទាប់មកបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុច (x 0 ; f (x 0)) ដែលមានមេគុណមុំ f '(x 0) ត្រូវបានគេហៅថាតង់សង់។

តើមានអ្វីកើតឡើងប្រសិនបើដេរីវេមិនមាននៅចំណុច x 0? មានជម្រើសពីរ៖

មិនមានតង់សង់ទៅនឹងក្រាហ្វទេ។ ឧទាហរណ៍បុរាណគឺមុខងារ y = |x | នៅចំណុច (0; 0) ។
តង់សង់ក្លាយជាបញ្ឈរ។ នេះជាការពិតឧទាហរណ៍សម្រាប់អនុគមន៍ y = arcsin x នៅចំណុច (1; π / 2) ។

សមីការតង់សង់

បន្ទាត់ត្រង់មិនបញ្ឈរណាមួយត្រូវបានផ្តល់ដោយសមីការនៃទម្រង់ y = kx + b ដែល k ជាជម្រាល។ តង់សង់គឺមិនមានករណីលើកលែងនោះទេ ហើយដើម្បីបង្កើតសមីការរបស់វានៅចំណុចមួយចំនួន x 0 វាគ្រប់គ្រាន់ដើម្បីដឹងពីតម្លៃនៃអនុគមន៍ និងដេរីវេនៅចំណុចនេះ។

ដូច្នេះសូមឱ្យអនុគមន៍ y = f (x) ត្រូវបានផ្តល់ឱ្យ ដែលមានដេរីវេ y = f '(x) នៅលើផ្នែក។ បន្ទាប់មកនៅចំណុចណាមួយ x 0 ∈ (a ; b) តង់សង់អាចត្រូវបានទាញទៅក្រាហ្វនៃអនុគមន៍នេះ ដែលត្រូវបានផ្តល់ដោយសមីការ៖

y = f '(x 0) (x − x 0) + f (x 0)

នៅទីនេះ f '(x 0) គឺជាតម្លៃនៃដេរីវេនៅចំនុច x 0 ហើយ f (x 0) គឺជាតម្លៃនៃអនុគមន៍។

កិច្ចការ។ អនុគមន៍ y = x 3 ។ សរសេរសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុច x 0 = 2 ។

សមីការតង់សង់៖ y = f '(x 0) · (x − x 0) + f (x 0) ។ ចំនុច x 0 = 2 ត្រូវបានផ្តល់ឱ្យយើង ប៉ុន្តែតម្លៃ f (x 0) និង f '(x 0) នឹងត្រូវគណនា។

ដំបូងយើងស្វែងរកតម្លៃនៃមុខងារ។ អ្វីគ្រប់យ៉ាងគឺងាយស្រួលនៅទីនេះ៖ f (x 0) = f (2) = 2 3 = 8;
ឥឡូវនេះ ចូរយើងស្វែងរកដេរីវេ៖ f '(x) = (x 3)' = 3x 2;
យើងជំនួស x 0 = 2 ទៅក្នុងដេរីវេ៖ f '(x 0) = f '(2) = 3 2 2 = 12;
សរុបយើងទទួលបាន៖ y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16 ។
នេះគឺជាសមីការតង់សង់។

កិច្ចការ។ សរសេរសមីការសម្រាប់តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f (x) = 2sin x + 5 នៅចំណុច x 0 = π /2 ។

លើកនេះ យើងនឹងមិនពណ៌នាអំពីសកម្មភាពនីមួយៗដោយលំអិតទេ - យើងនឹងបង្ហាញតែជំហានសំខាន់ៗប៉ុណ្ណោះ។ យើងមាន:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f '(x) = (2sin x + 5)' = 2cos x;
f '(x 0) = f '(π / 2) = 2cos (π / 2) = 0;

សមីការតង់សង់៖

y = 0 · (x − π / 2) + 7 ⇒ y = 7

ក្នុងករណីចុងក្រោយ បន្ទាត់ត្រង់ប្រែទៅជាផ្ដេក ពីព្រោះ មេគុណមុំរបស់វា k = 0 ។ មិនមានអ្វីខុសជាមួយនេះទេ - យើងគ្រាន់តែជំពប់ដួលលើចំណុចខ្លាំងមួយ។

ពិចារណារូបភាពខាងក្រោម៖

វាពិពណ៌នាអំពីមុខងារជាក់លាក់មួយ y = f(x) ដែលអាចខុសគ្នាត្រង់ចំនុច a ។ ចំណុច M ដែលមានកូអរដោណេ (a; f(a)) ត្រូវបានសម្គាល់។ អក្សរកាត់ MR ត្រូវបានគូរតាមរយៈចំណុចបំពាន P(a + ∆x; f(a + ∆x)) នៃក្រាហ្វ។

ប្រសិនបើឥឡូវនេះចំនុច P ត្រូវបានប្តូរតាមក្រាហ្វទៅចំណុច M នោះបន្ទាត់ត្រង់ MR នឹងបង្វិលជុំវិញចំណុច M។ ក្នុងករណីនេះ ∆x នឹងមានទំនោរទៅសូន្យ។ ពីទីនេះយើងអាចបង្កើតនិយមន័យនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍។

តង់សង់ទៅក្រាហ្វនៃអនុគមន៍

តង់សង់ទៅក្រាហ្វនៃអនុគមន៍គឺជាទីតាំងកំណត់នៃសេកាន ដោយសារការកើនឡើងនៃអាគុយម៉ង់មានទំនោរទៅសូន្យ។ វាគួរតែត្រូវបានយល់ថាអត្ថិភាពនៃដេរីវេនៃអនុគមន៍ f នៅចំណុច x0 មានន័យថានៅចំណុចនៃក្រាហ្វនេះមាន តង់សង់ទៅគាត់។

ក្នុងករណីនេះ មេគុណមុំនៃតង់សង់នឹងស្មើនឹងដេរីវេនៃអនុគមន៍នេះនៅចំណុច f'(x0)។ នេះគឺជាអត្ថន័យធរណីមាត្រនៃដេរីវេ។ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f ខុសគ្នាត្រង់ចំនុច x0 គឺជាបន្ទាត់ត្រង់ជាក់លាក់មួយឆ្លងកាត់ចំណុច (x0;f(x0)) និងមានមេគុណមុំ f'(x0)។

សមីការតង់សង់

ចូរយើងព្យាយាមទទួលបានសមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f នៅចំណុច A(x0; f(x0))។ សមីការនៃបន្ទាត់ត្រង់ជាមួយជម្រាល k មានទម្រង់ដូចខាងក្រោមៈ

ដោយសារមេគុណជម្រាលរបស់យើងគឺស្មើនឹងដេរីវេ f'(x0)បន្ទាប់មកសមីការនឹងយកទម្រង់ដូចខាងក្រោម៖ y = f'(x0)* x + ខ។

ឥឡូវយើងគណនាតម្លៃនៃ b ។ ដើម្បីធ្វើដូចនេះយើងប្រើការពិតដែលថាមុខងារឆ្លងកាត់ចំណុច A ។

f(x0) = f'(x0)*x0 + b ពីទីនេះយើងបង្ហាញ b និងទទួលបាន b = f(x0) - f'(x0)*x0 ។

យើងជំនួសតម្លៃលទ្ធផលទៅក្នុងសមីការតង់ហ្សង់៖

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x − x0)។

y = f(x0) + f'(x0)*(x − x0) ។

ពិចារណាឧទាហរណ៍ខាងក្រោម៖ រកសមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f(x) = x 3 - 2*x 2 + 1 នៅចំណុច x = 2 ។

2. f(x0) = f(2) = 2 2 − 2 * 2 2 + 1 = 1 ។

3. f'(x) = 3*x 2 − 4*x ។

4. f'(x0) = f'(2) = 3*2 2 − 4*2 = 4 ។

5. ជំនួសតម្លៃដែលទទួលបានទៅក្នុងរូបមន្តតង់សង់ យើងទទួលបាន៖ y = 1 + 4*(x − 2)។ ការបើកតង្កៀប និងនាំយកពាក្យស្រដៀងគ្នា យើងទទួលបាន៖ y = 4*x − 7 ។

ចម្លើយ៖ y = 4 * x − 7 ។

គ្រោងការណ៍ទូទៅសម្រាប់បង្កើតសមីការតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y = f(x)៖

1. កំណត់ x0 ។

2. គណនា f(x0)។

3. គណនា f'(x)

ពេញនិយម

Parthenogenesis - បច្ចេកទេសនៃការមានគភ៌ដែលមិនល្អឥតខ្ចោះ

« គោលគំនិតនៃ parthenogenesis កំឡុងពេលបង្កកំណើត មេជីវិតឈ្មោលបញ្ចេញពងចេញពីស្ថានភាពអសកម្មរបស់វា ហើយវាចាប់ផ្តើមអភិវឌ្ឍ។ ប៉ុន្តែនៅក្នុងធម្មជាតិមានករណី ... »

រឿងនិទានរបស់បងប្អូនបីនាក់ ដែលបានផ្តល់ឱ្យបងប្អូនប្រុសបីនាក់នូវគ្រឿងបន្លាស់ Harry Potter

« មានពេលមួយ មានបងប្អូនបីនាក់នៃអ្នកជំនួយការ ហើយថ្ងៃមួយ ពួកគេត្រូវឆ្លងទន្លេមួយ ពួកគេមិនអាចហែលឆ្លងកាត់វាបានឡើយ វាធំទូលាយ និងជ្រៅពេក។ ហើយបងប្អូន... »

De Broglie បានសន្មតថាភាគល្អិតនៃរូបធាតុ

« O.S.Ageeva, T.N.Stroganova, K.S.Chemezova ធាតុនៃមេកានិច QUANTUM និងរូបវិទ្យារដ្ឋរឹង Tyumen ។ 2009 UDC 537(075):621.38 Ageeva O.S.,... »