Жұмыс түрі: 7

Шарт

y=3x+2 түзуі y=-12x^2+bx-10 функциясының графигіне жанама. Жанасу нүктесінің абсциссасы нөлден кіші екенін ескере отырып, b табыңыз.

Шешімді көрсету

Шешім

y=-12x^2+bx-10 функциясының графигіндегі осы графикке жанама өтетін нүктенің абсциссасы x_0 болсын.

x_0 нүктесіндегі туындының мәні жанаманың еңісіне тең, яғни y"(x_0)=-24x_0+b=3. Екінші жағынан, жанама нүкте функцияның графигіне де, тангенс, яғни -12x_0^2+bx_0-10= 3x_0 + 2. Теңдеулер жүйесін аламыз. \бастау(жағдайлар) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \соңы(жағдайлар)

Бұл жүйені шеше отырып, біз x_0^2=1 аламыз, бұл не x_0=-1 немесе x_0=1 дегенді білдіреді. Абциссаның шарты бойынша жанасу нүктелері нөлден аз, сондықтан x_0=-1, онда b=3+24x_0=-21.

Жауап

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

y=-3x+4 түзуі y=-x^2+5x-7 функциясының графигіне жанамаға параллель. Жанасу нүктесінің абсциссасын табыңыз.

Шешімді көрсету

Шешім

Ерікті x_0 нүктесіндегі y=-x^2+5x-7 функциясының графигіне түзудің еңісі у"(x_0). Бірақ y"=-2x+5, сондықтан у"(x_0)=- 2x_0+5. Шартта көрсетілген y=-3x+4 түзуінің бұрыштық коэффициенті -3. Параллель түзулердің көлбеу коэффициенттері бірдей.Сондықтан =-2x_0 +5=-3 болатын x_0 мәнін табамыз.

Біз мынаны аламыз: x_0 = 4.

Жауап

Дереккөз: «Математика. Емтиханға дайындық-2017. профиль деңгейі. Ред. Ф.Ф.Лысенко, С.Ю.Кулабухова.

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

Шешімді көрсету

Шешім

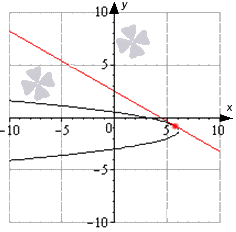
Суреттен жанаманың А(-6; 2) және В(-1; 1) нүктелері арқылы өтетінін анықтаймыз. x=-6 және y=1 түзулерінің қиылысу нүктесін С(-6; 1) арқылы, АВС бұрышын \alpha арқылы белгілеңіз (суреттен оның өткір екенін көруге болады). Сонда АВ түзуі Ox осінің оң бағытымен доғал \pi -\alpha бұрышын құрайды.

Өздеріңіз білетіндей, tg(\pi -\alpha) f(x) функциясының x_0 нүктесіндегі туындысының мәні болады. байқа, бұл tg \alpha =\frac(AC)(CB)=\frac(2-1)(-1-(-6))=\frac15.Осы жерден азайту формулалары арқылы біз мынаны аламыз: tg(\pi -\alpha) =-tg \alpha =-\frac15=-0,2.

Жауап

Дереккөз: «Математика. Емтиханға дайындық-2017. профиль деңгейі. Ред. Ф.Ф.Лысенко, С.Ю.Кулабухова.

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

y=-2x-4 түзуі y=16x^2+bx+12 функциясының графигіне жанама. Жанасу нүктесінің абсциссасы нөлден үлкен екенін ескере отырып, b табыңыз.

Шешімді көрсету

Шешім

y=16x^2+bx+12 функциясының графигіндегі нүктенің абсциссасы x_0 болсын, ол арқылы

осы графикке жанама.

x_0 нүктесіндегі туындының мәні жанаманың еңісіне тең, яғни y "(x_0)=32x_0+b=-2. Екінші жағынан, жанама нүкте функцияның графигіне де, тангенс, яғни 16x_0^2+bx_0+12=- 2x_0-4 Теңдеулер жүйесін аламыз \бастау(жағдайлар) 32x_0+b=-2,\\16x_0^2+bx_0+12=-2x_0-4. \соңы(жағдайлар)

Жүйені шеше отырып, біз x_0^2=1 аламыз, бұл не x_0=-1, не x_0=1 дегенді білдіреді. Абциссаның шарты бойынша жанасу нүктелері нөлден үлкен, сондықтан x_0=1, онда b=-2-32x_0=-34.

Жауап

Дереккөз: «Математика. Емтиханға дайындық-2017. профиль деңгейі. Ред. Ф.Ф.Лысенко, С.Ю.Кулабухова.

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

Суретте (-2; 8) интервалда анықталған y=f(x) функциясының графигі көрсетілген. Функция графигіне жанама y=6 түзуіне параллель болатын нүктелер санын анықтаңыз.

Шешімді көрсету

Шешім

y=6 түзуі Ox осіне параллель. Сондықтан функция графигіне жанама Ох осіне параллель болатын нүктелерді табамыз. Бұл диаграммада мұндай нүктелер экстремум нүктелері болып табылады (максималды немесе минималды ұпайлар). Көріп отырғаныңыздай, 4 экстремум нүктесі бар.

Жауап

Дереккөз: «Математика. Емтиханға дайындық-2017. профиль деңгейі. Ред. Ф.Ф.Лысенко, С.Ю.Кулабухова.

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

y=4x-6 түзуі y=x^2-4x+9 функциясының графигіне жанамаға параллель. Жанасу нүктесінің абсциссасын табыңыз.

Шешімді көрсету

Шешім

Ерікті x_0 нүктесіндегі y \u003d x ^ 2-4x + 9 функциясының графигіне жанаманың еңісі y "(x_0). Бірақ y" \u003d 2x-4, бұл у "(x_0) \ u003d 2x_0-4. Шартта көрсетілген y \u003d 4x-7 жанамасының еңісі 4-ке тең. Параллель түзулердің көлбеулері бірдей.Сондықтан 2x_0-4 \u003d 4 болатын x_0 мәнін табамыз. : x_0 \u003d 4.

Жауап

Дереккөз: «Математика. Емтиханға дайындық-2017. профиль деңгейі. Ред. Ф.Ф.Лысенко, С.Ю.Кулабухова.

Жұмыс түрі: 7
Тақырыбы: Туындының геометриялық мағынасы. Функция графигіне жанама

Шарт

Суретте y=f(x) функциясының графигі және абсцисса x_0 нүктесінде оған жанама көрсетілген. f(x) функциясының x_0 нүктесіндегі туындысының мәнін табыңыз.

Шешімді көрсету

Шешім

Суреттен жанаманың А(1; 1) және В(5; 4) нүктелері арқылы өтетінін анықтаймыз. C(5; 1) x=5 және y=1 түзулерінің қиылысу нүктесін, ал \alpha арқылы BAC бұрышын белгілеңіз (суреттен оның өткір екенін көруге болады). Сонда АВ түзуі Ox осінің оң бағытымен \alpha бұрышын құрайды.

Функция графигіне жанаманың теңдеуі

П.Романов, Т.Романова,
Магнитогорск,
Челябі облысы

Функция графигіне жанаманың теңдеуі

Мақала ITAKA+ қонақ үй кешенінің қолдауымен жарияланды. Северодвинск кеме жасаушылар қаласында тұрып, сіз уақытша баспана табу мәселесіне тап болмайсыз. , «ITAKA +» қонақ үй кешенінің http://itakaplus.ru сайтында сіз қалада кез келген мерзімге, күнделікті төлеммен пәтерді оңай және жылдам жалға ала аласыз.

Білім берудің қазіргі даму кезеңінде оның басты міндеттерінің бірі – шығармашылықпен ойлайтын жеке тұлғаны қалыптастыру. Оқушылардың шығармашылық қабілеттері ғылыми-зерттеу әрекетінің негіздеріне жүйелі түрде тартылған жағдайда ғана дамиды. Студенттердің шығармашылық күштерін, қабілеттері мен дарындарын пайдаланудың негізі толыққанды білім мен дағдыларды қалыптастырады. Осыған байланысты мектептегі математика курсының әрбір тақырыбы бойынша базалық білім мен дағды жүйесін қалыптастыру мәселесі де аз емес. Сонымен қатар толыққанды дағдылар жеке тапсырмалардың емес, олардың мұқият ойластырылған жүйесінің дидактикалық мақсаты болуы керек. Кең мағынада жүйе тұтастық пен тұрақты құрылымға ие, өзара байланысты өзара әрекеттесетін элементтердің жиынтығы ретінде түсініледі.

Студенттерге функция графигіне жанаманың теңдеуін құруға үйрету әдістемесін қарастырыңыз. Шын мәнінде, жанама теңдеуді табудың барлық тапсырмалары сызықтар жиынынан (парақ, отбасы) олардың белгілі бір талапты қанағаттандыратындарын таңдау қажеттілігіне дейін төмендейді - олар белгілі бір функцияның графигіне жанама болады. Бұл жағдайда таңдау жүзеге асырылатын жолдар жиынтығы екі жолмен көрсетілуі мүмкін:

а) xOy жазықтығында жатқан нүкте (түзулердің орталық қарындашы);
б) бұрыштық коэффициент (түзулердің параллель шоғыры).

Осыған байланысты жүйенің элементтерін оқшаулау мақсатында «Функция графигіне жанама» тақырыбын оқу барысында біз екі тапсырма түрін анықтадық:

1) жанама бойынша ол өтетін нүктемен берілген тапсырмалар;
2) тангенс бойынша оның көлбеуімен берілген тапсырмалар.

Тангенске есептер шығаруды үйрену А.Г. Мордкович. Оның бұрыннан белгілі болғанынан түбегейлі айырмашылығы жанама нүктесінің абциссасы а (х0 орнына) әрпімен белгіленеді, осыған байланысты жанама теңдеу пішінді алады.

y \u003d f (a) + f "(a) (x - a)

(салыстыру y \u003d f (x 0) + f "(x 0) (x - x 0)). Бұл әдістемелік әдіс, біздің ойымызша, студенттерге ағымдағы нүктенің координаталары қай жерде жазылғанын тез және оңай түсінуге мүмкіндік береді. жалпы тангенс теңдеуінде және жанасу нүктелері қайда орналасқан.

y = f(x) функциясының графигіне жанаманың теңдеуін құрастыру алгоритмі

1. Жанасу нүктесінің абсциссасын a әрпімен белгілеңіз.
2. f(a) мәнін табыңыз.
3. f "(x) және f "(a) табыңыз.
4. Табылған a, f (a), f "(a) сандарын y \u003d f (a) \u003d f "(a) (x - a) жанамасының жалпы теңдеуіне ауыстырыңыз.

Бұл алгоритмді оқушылардың амалдарды өз бетінше таңдауы және оларды орындау реттілігі негізінде құрастыруға болады.

Тәжірибе көрсеткендей, алгоритмді пайдалана отырып, әрбір негізгі есептің дәйекті шешімі функция графигіне жанама теңдеуін кезең-кезеңімен жазу мүмкіндігін қалыптастыруға мүмкіндік береді, ал алгоритм қадамдары әрекеттер үшін күшті нүктелер қызметін атқарады. . Бұл тәсіл П.Я әзірлеген психикалық әрекеттердің біртіндеп қалыптасу теориясына сәйкес келеді. Гальперин және Н.Ф. Талызына.

Тапсырмалардың бірінші түрінде екі негізгі міндет анықталды:

• жанама қисық сызықта жатқан нүкте арқылы өтеді (1-есеп);
• жанама қисық сызықта жатпайтын нүкте арқылы өтеді (2-есеп).

Тапсырма 1. Функция графигіне жанама теңестіріңіз М(3; – 2) нүктесінде.

Шешім. М(3; – 2) нүктесі жанасу нүктесі болып табылады, өйткені

1. a = 3 - жанасу нүктесінің абсциссасы.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 - жанама теңдеу.

2-тапсырма. М (- 3; 6) нүктесі арқылы өтетін у = - x 2 - 4x + 2 функциясының графигіне барлық жанамалардың теңдеулерін жазыңыз.

Шешім. M(– 3; 6) нүктесі жанама нүкте емес, өйткені f(– 3) 6 (Cурет 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - жанама теңдеу.

Тангенс М(– 3; 6) нүктесі арқылы өтеді, сондықтан оның координаталары жанама теңдеуді қанағаттандырады.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = - 4, a 2 = - 2.

Егер a = – 4 болса, онда жанама теңдеу у = 4х + 18 болады.

Егер a \u003d - 2 болса, онда жанама теңдеу y \u003d 6 түрінде болады.

Екінші түрдегі негізгі міндеттер мыналар болады:

• жанама қандай да бір түзуге параллель (3-есеп);
• жанама берілген түзуге қандай да бір бұрышпен өтеді (4-есеп).

3-тапсырма. y \u003d 9x + 1 түзуіне параллель y \u003d x 3 - 3x 2 + 3 функциясының графигіне барлық жанамалардың теңдеулерін жазыңыз.

Шешім.

1. а – жанасу нүктесінің абсциссасы.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Бірақ, екінші жағынан, f "(a) \u003d 9 (параллельдік шарты). Сонымен, біз 3a 2 - 6a \u003d 9 теңдеуін шешуіміз керек. Оның түбірлері a \u003d - 1, a \u003d 3 (Cурет 1). 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 - жанама теңдеу;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) у = 3 + 9(x - 3);

y = 9x – 24 – жанама теңдеу.

4-тапсырма. у = 0,5х 2 - 3х + 1 функциясының графигіне y = 0 түзуіне 45 ° бұрышпен өтетін жанаманың теңдеуін жазыңыз (4-сурет).

Шешім. f "(a) \u003d tg 45 ° шартынан біз мынаны табамыз: a - 3 \u003d 1^a=4.

1. a = 4 - жанасу нүктесінің абсциссасы.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - жанама теңдеуі.

Кез келген басқа есептің шешімі бір немесе бірнеше негізгі есептерді шешуге қысқартылатынын көрсету оңай. Мысал ретінде келесі екі мәселені қарастырыңыз.

1. Параболаға y = 2x 2 - 5x - 2 жанамаларының теңдеулерін жазыңыз, егер жанамалар тік бұрышта қиылыса және олардың біреуі абсцисса 3 нүктесінде параболаға тиіп тұрса (5-сурет).

Шешім. Жанасу нүктесінің абсциссасы берілгендіктен, шешімнің бірінші бөлігі түйінді есеп 1-ге келтіріледі.

1. a \u003d 3 - оң жақ бұрыштың бір жағының жанасу нүктесінің абсциссасы.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - бірінші жанаманың теңдеуі.

А болсын бірінші жанаманың көлбеу бұрышы болып табылады. Жанамалар перпендикуляр болғандықтан, екінші жанаманың көлбеу бұрышы болады. Бірінші жанаманың y = 7x – 20 теңдеуінен tg a = 7. Табыңыз

Бұл екінші жанаманың еңісі .

Одан әрі шешім 3-негізгі тапсырмаға келтіріледі.

B(c; f(c)) екінші түзудің жанама нүктесі болсын

1. - екінші жанасу нүктесінің абсциссасы.
2.
3.
4.
екінші жанаманың теңдеуі болып табылады.

Ескерту. Егер оқушылар перпендикуляр түзулердің k 1 k 2 = - 1 коэффициенттерінің қатынасын білсе, жанаманың еңісін оңай табуға болады.

2. Функция графиктерінің барлық ортақ жанамаларының теңдеулерін жазыңыз

Шешім. Тапсырма ортақ жанамалардың жанасу нүктелерінің абсциссаларын табуға, яғни 1 түйінді есепті жалпы түрде шешуге, теңдеулер жүйесін құрастырып, содан кейін оны шешуге (6-сурет).

1. y = x 2 + x + 1 функциясының графигінде жатқан жанасу нүктесінің абсциссасы а болсын.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.

1. Функция графигінде жатқан жанама нүктесінің абциссасы с болсын
2.
3. f "(c) = c.
4.

Жанамалар ортақ болғандықтан

Сонымен y = x + 1 және y = - 3x - 3 ортақ жанамалар.

Қарастырылып отырған тапсырмалардың негізгі мақсаты – белгілі бір зерттеу дағдыларын (талдау, салыстыру, жалпылау, гипотеза қою және т.б.) талап ететін күрделірек тапсырмаларды шешу кезінде оқушыларды негізгі тапсырманың түрін өзін-өзі тануға дайындау. Мұндай тапсырмаларға негізгі тапсырма компонент ретінде енгізілген кез келген тапсырма жатады. Мысал ретінде функцияны оның жанамаларының тобынан табу есебін (1-есепке кері) қарастырайық.

3. y = x 2 + bx + c функциясының графигіне y \u003d x және y \u003d - 2x сызықтары қандай b және c үшін жанама болады?

Шешім.

y = x түзуінің у = x 2 + bx + c параболасымен жанасу нүктесінің абсциссасы t болсын; p – y = - 2x түзуінің у = x 2 + bx + c параболасымен жанасу нүктесінің абсциссасы. Сонда у = х жанама теңдеуі y = (2t + b)x + c - t 2, ал у = - 2x жанама теңдеуі у = (2p + b)x + c - p 2 түрінде болады. .

Теңдеулер жүйесін құрастыру және шешу

Жауап:

Өз бетінше шешуге арналған тапсырмалар

1. Графиктің у = х + 3 түзуімен қиылысу нүктелеріндегі у = 2х 2 - 4х + 3 функциясының графигіне салынған жанамалардың теңдеулерін жазыңыз.

Жауап: y \u003d - 4x + 3, y \u003d 6x - 9,5.

2. y \u003d x 2 - абсциссасы бар графиктің нүктесіндегі ax функциясының графигіне сызылған жанама а-ның қандай мәндері үшін M (2; 3) нүктесі арқылы өтеді. ?

Жауабы: a = 0,5.

3. y = px - 5 сызығы p-тің қандай мәндері үшін у = 3x 2 - 4x - 2 қисығына тиеді?

Жауап: p 1 \u003d - 10, p 2 \u003d 2.

4. y = 3x - x 3 функциясының графигінің барлық ортақ нүктелерін және осы графикке Р(0; 16) нүктесі арқылы жүргізілген жанаманы табыңыз.

Жауабы: А(2; - 2), В(- 4; 52).

5. y = x 2 + 6x + 10 параболасы мен түзудің арасындағы ең қысқа қашықтықты табыңыз.

Жауап:

6. y \u003d x 2 - x + 1 қисығында графиктің жанамасының y - 3x + 1 \u003d 0 түзуіне параллель болатын нүктесін табыңыз.

Жауабы: М(2; 3).

7. у = x 2 + 2x - функциясының графигіне жанаманың теңдеуін жазыңыз. 4x | бұл оған екі нүктеде тиеді. Сурет салу.

Жауабы: у = 2х - 4.

8. y = 2x – 1 түзуінің у = x 4 + 3x 2 + 2x қисығымен қиылыспайтынын дәлелдеңдер. Олардың ең жақын нүктелерінің арасындағы қашықтықты табыңыз.

Жауап:

9. y \u003d x 2 параболада абсциссалары x 1 \u003d 1, x 2 \u003d 3 болатын екі нүкте алынады.Осы нүктелер арқылы секант сызылады. Параболаның қай нүктесінде оған жанама жүргізілген секантқа параллель болады? Секант пен жанаманың теңдеулерін жазыңыз.

Жауап: y \u003d 4x - 3 - секант теңдеуі; y = 4x – 4 – жанама теңдеу.

10. q бұрышын табыңыз 0 және 1 абсциссалары бар нүктелерде сызылған y \u003d x 3 - 4x 2 + 3x + 1 функциясының графигіне жанамалардың арасында.

Жауабы: q = 45°.

11. Функция графигіне жанама қандай нүктелерде Ox осімен 135° бұрыш жасайды?

Жауабы: А(0; - 1), В(4; 3).

12. А(1; 8) нүктесінде қисыққа дейін жанама сызылады. Координаталық осьтер арасына салынған жанама кесіндінің ұзындығын табыңыз.

Жауап:

13. y \u003d x 2 - x + 1 және y \u003d 2x 2 - x + 0,5 функцияларының графиктеріне барлық ортақ жанамалардың теңдеуін жазыңыз.

Жауабы: у = - 3х және у = х.

14. Функция графигіне жанамалардың арасындағы қашықтықты табыңыз х осіне параллель.

Жауап:

15. y \u003d x 2 + 2x - 8 параболасы х осін қандай бұрыштармен қиып өтетінін анықтаңыз.

Жауап: q 1 \u003d арктан 6, q 2 \u003d арктан (- 6).

16. Функция графигі бойынша Барлық нүктелерді табыңыз, олардың әрқайсысында осы графикке жанама координаталардың оң жарты осьтерін қиып, олардан тең кесінділерді кесіп тастайды.

Жауабы: A(-3; 11).

17. y = 2x + 7 түзуі мен у = x 2 – 1 параболасы M және N нүктелерінде қиылысады. M және N нүктелеріндегі параболаға жанама түзулердің К қиылысу нүктесін табыңыз.

Жауабы: K(1; - 9).

18. b-ның қандай мәндері үшін y \u003d 9x + b сызығы y \u003d x 3 - 3x + 15 функциясының графигіне жанама болады?

Жауабы: - 1; 31.

19. k-ның қандай мәндері үшін y = kx – 10 түзуінің у = 2x 2 + 3x – 2 функциясының графигімен бір ғана ортақ нүктесі бар? Табылған k мәндері үшін нүктенің координаталарын анықтаңыз.

Жауабы: k 1 = - 5, A(- 2; 0); k 2 = 11, B(2; 12).

20. М(1; 8) нүктесі арқылы абсцисса x 0 = 2 нүктесінде у = bx 3 – 2x 2 – 4 функциясының графигіне салынған жанама b-ның қандай мәндері үшін өтеді?

Жауабы: b = - 3.

21. Х осінде төбесі бар парабола В нүктесінде А(1; 2) және В(2; 4) нүктелері арқылы өтетін түзуге жанама. Парабола теңдеуін табыңыз.

Жауап:

22. y \u003d x 2 + kx + 1 параболасы k коэффициентінің қандай мәнінде Ox осіне тиеді?

Жауабы: k = q 2.

23. у = x + 2 түзуі мен у = 2х 2 + 4х - 3 қисығы арасындағы бұрыштарды табыңыз.

29. 45 ° бұрышта Ox осінің оң бағыты бар функция генераторларының графигіне жанамалардың арасындағы қашықтықты табыңыз.

Жауап:

30. y = x 2 + ax + b түріндегі барлық параболалардың у = 4x - 1 түзуіне тиетін төбелерінің локусын табыңыз.

Жауабы: у = 4х + 3 түзу.

Әдебиет

1. Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра және талдаудың бастаулары: мектеп оқушылары мен университет талапкерлеріне арналған 3600 есеп. - М., Бустард, 1999 ж.
2. Мордкович А. Жас мұғалімдерге арналған төртінші семинар. Тақырыбы: «Туынды қолданбалар». - М., «Математика», No21/94.
3. Психикалық әрекеттерді бірте-бірте ассимиляциялау теориясы негізінде білім мен дағдыны қалыптастыру. / Ред. П.Я. Гальперин, Н.Ф. Талызына. - М., Мәскеу мемлекеттік университеті, 1968 ж.

Мақалада графикалық белгілермен туындының геометриялық мағынасы, анықтамалары толық түсіндіріледі. Жанама түзудің теңдеуі мысалдар арқылы қарастырылады, 2-ші ретті қисықтарға жанаманың теңдеулері табылады.

Yandex.RTB R-A-339285-1 Анықтама 1

y \u003d k x + b түзу сызығының көлбеу бұрышы α бұрышы деп аталады, ол х осінің оң бағытынан y \u003d k x + b түзуіне оң бағытта өлшенеді.

Суретте өгіздің бағыты жасыл жебемен және жасыл доғамен, ал көлбеу бұрышы қызыл доғамен көрсетілген. Көк сызық түзу сызықты білдіреді.

Анықтама 2

y \u003d k x + b түзуінің еңісі сандық коэффициент k деп аталады.

Еңіс түзудің еңісіне тең, басқаша айтқанда k = t g α .

• Түзу сызықтың еңісі тек o x параллель және көлбеу нөлге тең болғанда ғана 0 болады, өйткені нөлдің тангенсі 0-ге тең. Сонымен, теңдеудің түрі у = b болады.
• y = k x + b түзуінің көлбеу бұрышы өткір болса, онда 0 шарттары.< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , ал графикте өсу байқалады.
• Егер α \u003d π 2 болса, онда түзудің орналасуы x-ке перпендикуляр болады. Теңдік c нақты сан болатын x = c теңдігімен белгіленеді.
• y = k x + b түзуінің көлбеу бұрышы доғал болса, онда ол π 2 шарттарына сәйкес келеді.< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Анықтама 3

Секант - f (x) функциясының 2 нүктесі арқылы өтетін түзу. Басқаша айтқанда, секант деп берілген функцияның графигіндегі кез келген екі нүкте арқылы өтетін түзуні айтады.

Суретте A B - секант, ал f (x) - қара қисық, α - қызыл доға, секанттың көлбеу бұрышын көрсетеді.

Түзу сызықтың еңісі көлбеу бұрышының тангенсіне тең болғанда, тікбұрышты үшбұрыштың A B C тангенсін көршілес үшбұрышқа қарама-қарсы катетке қатысты табуға болатыны анық.

Анықтама 4

Пішіннің секантын табу формуласын аламыз:

k = tg α = BCAC = f (x B) - fx A x B - x A , мұндағы А және В нүктелерінің абсциссалары x A , x B , және f (x A) , f (x) мәндері B) осы нүктелердегі мәндік функциялар.

Секанттың еңісі k \u003d f (x B) - f (x A) x B - x A немесе k \u003d f (x A) - f (x B) x A - x теңдігі арқылы анықталады. B, және теңдеу y = f (x B) - f (x A) x B - x A x - x A + f (x A) түрінде жазылуы керек немесе
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Секант графикті визуалды түрде 3 бөлікке бөледі: А нүктесінің сол жағына, А нүктесінен В-ға дейін, В-ның оң жағына. Төмендегі суретте бірдей деп саналатын үш секант бар екендігі көрсетілген, яғни олар ұқсас теңдеуді пайдаланып орнатыңыз.

Анықтама бойынша бұл жағдайда сызық пен оның секанты сәйкес келетіні анық.

Секант берілген функцияның графигін бірнеше рет қиып өте алады. Егер секант үшін y \u003d 0 түріндегі теңдеу болса, онда синусоидпен қиылысу нүктелерінің саны шексіз болады.

Анықтама 5

x 0 нүктесіндегі f (x) функциясының графигіне жанама; f (x 0) берілген х 0 нүктесі арқылы өтетін түзу деп аталады; f (x 0) , х 0-ге жақын көптеген x мәндері бар сегменттің қатысуымен.

1-мысал

Төмендегі мысалды толығырақ қарастырайық. Сонда y = x + 1 функциясымен берілген түзу координаталары (1 ; 2) нүктесінде у = 2 х-қа жанама болып есептелетінін көруге болады. Түсінікті болу үшін мәндері (1; 2) жақын графиктерді қарастыру қажет. y = 2 x функциясы қара түспен белгіленген, көк сызық жанама, қызыл нүкте - қиылысу нүктесі.

Әлбетте, y \u003d 2 x y \u003d x + 1 сызығымен біріктіріледі.

Тангенсті анықтау үшін В нүктесі А нүктесіне шексіз жақындаған кездегі A B жанамасының әрекетін қарастыру керек.Түсінікті болу үшін фигураны ұсынамыз.

Көк сызықпен көрсетілген A B секантасы жанаманың өзіне бейім болады, ал α секантының көлбеу бұрышы жанаманың өзінің α х көлбеу бұрышына жақындай бастайды.

Анықтама 6

А нүктесіндегі y \u003d f (x) функциясының графигіне жанама - бұл А-ға ұмтылатын A B секантының В нүктесіндегі шекті орны, яғни B → A.

Енді функцияның нүктедегі туындысының геометриялық мағынасын қарастыруға көшеміз.

f (x) функциясы үшін АВ секантын қарастыруға көшейік, мұндағы А және В координаталары x 0, f (x 0) және x 0 + ∆ x, f (x 0 + ∆ x), және ∆ x аргументтің өсімі ретінде белгіленеді. Енді функция ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) түрінде болады. Түсінікті болу үшін мысал ретінде суретті алайық.

Алынған тікбұрышты үшбұрышты қарастырайық A B C. Шешім үшін жанама анықтамасын қолданамыз, яғни ∆ y ∆ x = t g α қатынасын аламыз. Тангенс анықтамасынан lim ∆ x → 0 ∆ y ∆ x = t g α x болатыны шығады. Нүктедегі туынды ережеге сәйкес, х 0 нүктесіндегі f (x) туындысы функция өсімінің аргумент өсіміне қатынасының шегі деп аталады, мұндағы ∆ x → 0, онда f (x 0) = lim ∆ x → 0 ∆ y ∆ x деп белгіленеді.

Бұдан f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x болатыны шығады, мұндағы k x жанаманың еңісі ретінде белгіленеді.

Яғни, біз f ' (x) x 0 нүктесінде болуы мүмкін екенін аламыз және функцияның берілген графигінің жанасуы сияқты x 0 , f 0 (x 0) тең жанасу нүктесінде, мұндағы мән нүктедегі жанаманың еңісі х 0 нүктесіндегі туындыға тең. Сонда біз k x = f "(x 0) аламыз.

Функцияның нүктедегі туындысының геометриялық мағынасы сол нүктедегі графқа жанаманың бар екендігі туралы түсінік беріледі.

Жазықтықтағы кез келген түзудің теңдеуін жазу үшін оның өтетін нүктесімен көлбеу болуы керек. Оның белгіленуі қиылысында x 0 ретінде қабылданады.

x 0, f 0 (x 0) нүктесіндегі y \u003d f (x) функциясының графигіне жанама теңдеуі y \u003d f "(x 0) x - x 0 + f (x) пішінін алады. 0) .

Бұл f "(x 0) туындысының соңғы мәні жанаманың орнын анықтай алатынын білдіреді, яғни lim x → x 0 + 0 f" (x) = ∞ және lim x → x 0 жағдайында вертикальды түрде. - 0 f "(x ) = ∞ немесе lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) шарты бойынша мүлде болмауы.

Тангенстің орналасуы оның көлбеуінің мәніне байланысты kx \u003d f "(x 0). Х осіне параллель болғанда, біз бұл kk \u003d 0, шамамен y - kx \u003d ∞ параллель болғанда аламыз, және x \u003d x 0 тангенс теңдеуінің түрі kx > 0 кезінде артады, kx болған сайын азаяды< 0 .

2-мысал

y \u003d ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 функциясының графигіне жанама теңдеуін координаталары (1; 3) нүктедегі бұрыштың анықтамасымен құрастырыңыз. бейімділік.

Шешім

Болжам бойынша, функция барлық нақты сандар үшін анықталған. (1 ; 3) шартымен көрсетілген координаталары бар нүкте түйісу нүктесі, онда x 0 = - 1 , f (x 0) = - 3 болатынын аламыз.

Мәні - 1 болатын нүктедегі туындыны табу керек. Біз мұны түсінеміз

y "= ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" == ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = ex + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Жанасу нүктесіндегі f ’ (x) мәні еңістің тангенсіне тең жанаманың еңісі болып табылады.

Сонда k x = t g α x = y "(x 0) = 3 3

Бұдан α x = a r c t g 3 3 = π 6 болатыны шығады

Жауап:жанама теңдеу формасын алады

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

Түсінікті болу үшін біз графикалық иллюстрацияда мысал келтіреміз.

Бастапқы функцияның графигі үшін қара түс пайдаланылады, көк түс жанама кескін, қызыл нүкте сенсорлық нүкте болып табылады. Оң жақтағы сурет үлкейтілген көріністі көрсетеді.

3-мысал

Берілген функцияның графигіне жанаманың бар екенін табыңыз
y = 3 x - 1 5 + 1 координаталары бар нүктеде (1 ; 1) . Теңдеу жазыңыз және көлбеу бұрышын анықтаңыз.

Шешім

Болжам бойынша, берілген функцияның анықталу облысы барлық нақты сандар жиыны болып табылады.

Туындыны табуға көшейік

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Егер x 0 = 1 , онда f ' (x) анықталмайды, бірақ шектер lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 түрінде жазылады. 5 1 + 0 = + ∞ және lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , бұл нүктедегі тік тангенстің болуын білдіреді. нүкте (1 ; 1) .

Жауап:теңдеу x \u003d 1 пішінін алады, мұнда көлбеу бұрышы π 2-ге тең болады.

Түсінікті болу үшін графигін салайық.

4-мысал

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 функциясының графигінің нүктелерін табыңыз, мұндағы

1. Тангенс жоқ;
2. Тангенс х-ке параллель;
3. Тангенс y = 8 5 x + 4 түзуіне параллель.

Шешім

Анықтау саласына назар аудару қажет. Болжам бойынша, функция барлық нақты сандар жиынында анықталған. Модульді кеңейтіп, x ∈ - ∞ аралықтары бар жүйені шешіңіз; 2 және [- 2; +∞) . Біз мұны түсінеміз

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

Функцияны ажырату керек. Бізде бұл бар

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

x = - 2 болғанда туынды болмайды, себебі бір жақты шектеулер сол нүктеде тең емес:

lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Біз функцияның мәнін x \u003d - 2 нүктесінде есептейміз, оны аламыз

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, яғни жанама (- 2; - 2) нүктесі болмайды.
2. Көлбеу нөлге тең болғанда тангенс х-ке параллель болады. Содан кейін kx \u003d tg α x \u003d f "(x 0). Яғни, функцияның туындысы оны нөлге айналдырғанда, мұндай х мәндерін табу керек. Яғни, мәндер f '(x) және жанасу нүктелері болады, онда жанама шамамен x параллель болады.

x ∈ - ∞ болғанда; - 2 , онда - 1 5 (x 2 + 12 x + 35) = 0 , ал x ∈ (- 2 ; + ∞) үшін 1 5 (x 2 - 4 x + 3) = 0 аламыз.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Функцияның сәйкес мәндерін есептейміз

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 ж 3 = у (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 ж 4 = у (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Демек - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 функция графигінің қажетті нүктелері болып саналады.

Шешімнің графикалық көрінісін қарастырыңыз.

Қара сызық – функцияның графигі, қызыл нүктелер – жанасу нүктелері.

1. Түзулер параллель болса, көлбеулер тең болады. Содан кейін функция графигінің еңісі 8 5 мәніне тең болатын нүктелерін іздеу керек. Ол үшін у "(х) = 8 5 түріндегі теңдеуді шешу керек. Сонда x ∈ - ∞; - 2 болса, мынаны аламыз - 1 5 (x 2 + 12 x + 35) = 8 5, ал егер x ∈ ( - 2 ; + ∞) болса, онда 1 5 (x 2 - 4 x + 3) = 8 5 .

Бірінші теңдеудің түбірі жоқ, себебі дискриминант нөлден кіші. Соны жазып алайық

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Басқа теңдеудің екі нақты түбірі бар

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Функцияның мәндерін табуға көшейік. Біз мұны түсінеміз

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Мәндері бар ұпайлар - 1 ; 4 15, 5; 8 3 - жанамалары у = 8 5 x + 4 түзуіне параллель болатын нүктелер.

Жауап:қара сызық - функция графигі, қызыл сызық - граф y \u003d 8 5 x + 4, көк сызық - нүктелердегі жанамалар - 1; 4 15, 5; 8 3 .

Берілген функциялар үшін жанамалардың шексіз санының болуы мүмкін.

5-мысал

y = - 2 x + 1 2 түзуіне перпендикуляр болатын y = 3 cos 3 2 x - π 4 - 1 3 функциясының барлық қолда бар жанамаларының теңдеулерін жазыңыз.

Шешім

Тангенс теңдеуін құру үшін түзулердің перпендикулярлық шартына сүйене отырып, жанасу нүктесінің коэффициенті мен координаталарын табу керек. Анықтама былай естіледі: түзулерге перпендикуляр еңістердің көбейтіндісі - 1-ге тең, яғни k x · k ⊥ = - 1 түрінде жазылады. Шарттан көлбеу түзуге перпендикуляр және k ⊥ = - 2 тең болса, онда k x = - 1 k ⊥ = - 1 - 2 = 1 2 болады.

Енді жанасу нүктелерінің координаталарын табу керек. Берілген функция үшін х мәнін табу керек, одан кейін оның мәні. Нүктедегі туындының геометриялық мағынасынан екенін ескеріңіз
x 0 біз k x \u003d y "(x 0) аламыз. Осы теңдіктен біз жанасу нүктелері үшін x мәндерін табамыз.

Біз мұны түсінеміз

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 2 x 0 - 4 = - 1 9

Бұл тригонометриялық теңдеу жанасу нүктелерінің ординаталарын есептеу үшін пайдаланылады.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk немесе 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk немесе 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk немесе x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z – бүтін сандар жиыны.

x байланыс нүктесі табылды. Енді y мәндерін іздеуге өту керек:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 немесе y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 немесе y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 немесе y 0 = - 4 5 + 1 3

Осыдан 2 3 π 4 - a r c sin 1 9 + 2 πk болатынын аламыз; 4 5 - 1 3, 2 3 5 π 4 + a r c sin 1 9 + 2 πk; - 4 5 + 1 3 - жанасу нүктелері.

Жауап:қажетті теңдеулер былай жазылады

y = 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Көрнекі көрініс үшін координаталық түзудегі функция мен жанаманы қарастырыңыз.

Суретте функцияның орны [ - 10 ; 10 ] , мұндағы қара сызық функцияның графигі, көк сызықтар y = - 2 x + 1 2 түріндегі берілген түзуге перпендикуляр болатын жанамалар. Қызыл нүктелер жанасу нүктелері болып табылады.

2-ші ретті қисықтардың канондық теңдеулері бір мәнді функциялар емес. Олар үшін жанама теңдеулер белгілі схемалар бойынша құрастырылады.

Шеңберге жанама

Центрі x c e n t e r нүктесінде орналасқан шеңберді орнату үшін; y c e n t e r және радиусы R, x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 формуласы қолданылады.

Бұл теңдікті екі функцияның бірігуі ретінде жазуға болады:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Бірінші функция суретте көрсетілгендей жоғарыда, екіншісі төменгі жағында.

x 0 нүктесіндегі шеңбердің теңдеуін құру; y 0 , ол жоғарғы немесе төменгі жарты шеңберде орналасқан, y \u003d R 2 - x - xcenter 2 + ycenter немесе y \u003d - R 2 - x - xcenter 2 + түріндегі функция графигінің теңдеуін табу керек. yцентрі көрсетілген нүктеде.

x c e n t e r нүктелерінде болғанда; y c e n t e r + R және x c e n t e r ; y c e n t e r - R тангенстерін y = y c e n t e r + R және y = y c e n t e r - R теңдеулері арқылы және x c e n t e r + R нүктелерінде беруге болады; y c e n t e r және
x c e n t e r - R ; y c e n t e r y шамасында параллель болады, онда x = x c e n t e r + R және x = x c e n t e r - R түріндегі теңдеулерді аламыз.

Эллипске жанама

Эллипс x c e n t e r центрінде болғанда; y c e n t e r a және b жарты осьтері бар болса, онда оны x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 теңдеуімен беруге болады.

Эллипс пен шеңберді екі функцияны, атап айтқанда, жоғарғы және төменгі жартылай эллипсті біріктіру арқылы белгілеуге болады. Сонда біз оны аламыз

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

Егер жанамалар эллипстің төбелерінде орналасса, онда олар шамамен х немесе шамамен у параллель болады. Түсінікті болу үшін төмендегі суретті қарастырыңыз.

6-мысал

Эллипстің x - 3 2 4 + y - 5 2 25 = 1 теңдеуін х мәндері x = 2-ге тең нүктелерінде жазыңыз.

Шешім

x = 2 мәніне сәйкес келетін жанасу нүктелерін табу керек. Эллипстің бар теңдеуіне ауыстыруды жасаймыз және оны аламыз

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ у = ± 5 3 2 + 5

Содан кейін 2; 5 3 2 + 5 және 2 ; - 5 3 2 + 5 - жоғарғы және төменгі жартылай эллипске жататын жанама нүктелер.

Эллипстің у-ға қатысты теңдеуін табуға және шешуге көшейік. Біз мұны түсінеміз

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 у = 5 ± 5 2 4 - x - 3 2

Жоғарғы жартылай эллипс y = 5 + 5 2 4 - x - 3 2, ал төменгісі y = 5 - 5 2 4 - x - 3 2 түріндегі функция арқылы нақтыланатыны анық.

Нүктедегі функцияның графигіне жанаманың теңдеуін тұжырымдау үшін стандартты алгоритмді қолданамыз. 2 нүктедегі бірінші жанаманың теңдеуін жазамыз; 5 3 2 + 5 сияқты болады

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Осы нүктедегі мәнмен екінші жанаманың теңдеуін аламыз
2; - 5 3 2 + 5 болады

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x) - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Графикалық түрде жанамалар келесідей белгіленеді:

Гиперболаға жанама

Гиперболаның центрі х c e n t e r нүктесінде болғанда; y c e n t e r және төбелері x c e n t e r + α ; y c e n t e r және x c e n t e r - α ; y c e n t e r , x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 теңсіздігі берілген, егер төбелері x c e n t e r болса; y c e n t e r + b және x c e n t e r ; y c e n t e r - b онда x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 теңсіздігімен беріледі.

Гиперболаны пішіннің екі біріктірілген функциясы ретінде көрсетуге болады

y = ba (x - xцентр) 2 - a 2 + yцентр = - ba (x - xcenter) 2 - a 2 + yцентр немесе y = ba (x - xcenter) 2 + a 2 + yцентр = - ba (x - xcenter) ) 2 + a 2 + yцентр

Бірінші жағдайда, бізде жанамалар у-ға параллель, ал екіншісінде олар х-ке параллель болады.

Бұдан шығатыны, гиперболаға жанаманың теңдеуін табу үшін жанама нүктесі қай функцияға жататынын анықтау керек. Мұны анықтау үшін теңдеулерде ауыстыруды жасап, олардың сәйкестігін тексеру қажет.

7-мысал

7 нүктедегі х - 3 2 4 - у + 3 2 9 = 1 гиперболаға жанаманың теңдеуін жаз; - 3 3 - 3 .

Шешім

Гиперболаны табу шешімі жазбасын 2 функцияны пайдаланып түрлендіру керек. Біз мұны түсінеміз

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 немесе y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Координатасы 7 берілген нүкте қай функцияға жататынын табу керек; - 3 3 - 3 .

Әлбетте, бірінші функцияны тексеру үшін y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 қажет болса, онда нүкте графикке жатпайды, өйткені теңдік орындалмайды.

Екінші функция үшін бізде y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , бұл нүктенің берілген графикке жататынын білдіреді. Осы жерден көлбеу коэффициентін табу керек.

Біз мұны түсінеміз

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ kx = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Жауап:тангенс теңдеуін келесідей көрсетуге болады

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Ол келесідей бейнеленеді:

Параболаға жанама

x 0, y (x 0) нүктесінде y \u003d ax 2 + bx + c параболасына жанама теңдеуін құру үшін стандартты алгоритмді пайдалану керек, содан кейін теңдеу y \u003d y пішінін алады. (x 0) x - x 0 + y ( x 0) Төбедегі мұндай жанама х-ке параллель болады.

x = a y 2 + b y + c параболасын екі функцияның бірігуі ретінде анықтау керек. Сондықтан у үшін теңдеуді шешу керек. Біз мұны түсінеміз

x = ay 2 + by + c ⇔ ay 2 + by + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 ay = - b - b 2 - 4 a (c - x) 2 a

Оның графигін былайша салайық:

x 0 , y (x 0) нүктелерінің функцияға жататынын анықтау үшін стандартты алгоритмді ақырын орындаңыз. Мұндай жанама параболаға қатысты у-ға параллель болады.

8-мысал

Бізде 150 ° тангенс көлбеу болғанда х - 2 у 2 - 5 у + 3 графигіне жанаманың теңдеуін жазыңыз.

Шешім

Шешімді параболаны екі функция ретінде көрсетуден бастаймыз. Біз мұны түсінеміз

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 xy = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Еңістің мәні осы функцияның х 0 нүктесіндегі туындының мәніне тең және еңістің тангенсіне тең.

Біз алып жатырмыз:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

Осы жерден жанасу нүктелері үшін х мәнін анықтаймыз.

Бірінші функция былай жазылады

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Теріс мән алғандықтан, нақты тамырлар жоқ екені анық. Біз мұндай функция үшін 150 ° бұрышпен жанама жоқ деген қорытындыға келдік.

Екінші функция былай жазылады

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Бізде жанасу нүктелері бар - 23 4 ; - 5 + 3 4 .

Жауап:жанама теңдеу формасын алады

у = - 1 3 x - 23 4 + - 5 + 3 4

Оның графигін былай салайық:

Мәтінде қатені байқасаңыз, оны бөлектеп, Ctrl+Enter пернелерін басыңыз

Қандай да бір х 0 нүктесінде соңғы f (x 0) туындысы болатын f функциясы берілсін. Сонда (x 0; f (x 0)) нүктесі арқылы өтетін, f '(x 0) көлбеуі бар түзу жанама деп аталады.

Бірақ x 0 нүктесіндегі туынды болмаса не болады? Екі нұсқа бар:

1. Графикке жанама да жоқ. Классикалық мысал y = |x | функциясы болып табылады нүктесінде (0; 0).
2. Тангенс тік болады. Бұл дұрыс, мысалы, (1; π /2) нүктесіндегі y = arcsin x функциясы үшін.

Тангенс теңдеуі

Кез келген тік емес түзу y = kx + b түріндегі теңдеу арқылы беріледі, мұндағы k – еңіс. Тангенс ерекшелік емес, оның қандай да бір х 0 нүктесінде теңдеуін құру үшін осы нүктедегі функцияның мәні мен туындысын білу жеткілікті.

Сонымен, сегментте y \u003d f '(x) туындысы бар y \u003d f (x) функциясы берілсін. Сонда кез келген x 0 ∈ (a; b) нүктесінде осы функцияның графигіне жанама салуға болады, ол мына теңдеумен берілген:

y \u003d f '(x 0) (x - x 0) + f (x 0)

Мұнда f ’(x 0) – х 0 нүктесіндегі туындының мәні, ал f (x 0) – функцияның өзінің мәні.

Тапсырма. y = x 3 функциясы берілген. Осы функцияның х 0 = 2 нүктесіндегі графигіне жанама теңдеуін жазыңыз.

Тангенс теңдеуі: y \u003d f '(x 0) (x - x 0) + f (x 0). Бізге x 0 = 2 нүктесі берілген, бірақ f (x 0) және f '(x 0) мәндерін есептеу керек болады.

Алдымен функцияның мәнін табайық. Мұнда бәрі оңай: f (x 0) = f (2) = 2 3 = 8;
Енді туындыны табайық: f '(x) \u003d (x 3) ' \u003d 3x 2;
x 0 = 2 туындысында алмастыру: f '(x 0) = f '(2) = 3 2 2 = 12;
Сонымен мынаны аламыз: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
Бұл жанама теңдеу.

Тапсырма. x 0 \u003d π / 2 нүктесіндегі f (x) \u003d 2sin x + 5 функциясының графигіне жанама теңдеуін құрыңыз.

Бұл жолы біз әрбір әрекетті егжей-тегжейлі сипаттамаймыз - біз тек негізгі қадамдарды көрсетеміз. Бізде бар:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 \u003d 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

Тангенс теңдеуі:

y = 0 (x − π /2) + 7 ⇒ y = 7

Соңғы жағдайда сызық көлденең болып шықты, өйткені Оның еңісі k = 0. Бұл жерде қате жоқ - біз жай ғана экстремум нүктесіне тап болдық.

Келесі суретті қарастырыңыз:

Ол а нүктесінде дифференциалданатын кейбір y = f(x) функциясын көрсетеді. Координаталары (a; f(a)) белгіленген М нүктесі. Графиктің еркін P(a + ∆x; f(a + ∆x)) нүктесі арқылы секант МП сызылады.

Егер енді Р нүктесі график бойымен М нүктесіне жылжытылса, онда MP түзу M нүктесінің айналасында айналады. Бұл жағдайда ∆x нөлге ұмтылады. Осы жерден функция графигіне жанаманың анықтамасын тұжырымдауға болады.

Функция графигіне жанама

Функция графигіне жанама деп аргумент өсімі нөлге ұмтылған кездегі секанттың шекті орны болып табылады. x0 нүктесінде f функциясының туындысының болуы графиктің осы нүктесінде болатынын білдіреді деп түсіну керек. жанамаоған.

Бұл жағдайда жанаманың көлбеуі осы f'(x0) нүктесіндегі осы функцияның туындысына тең болады. Бұл туындының геометриялық мағынасы. x0 нүктесінде дифференциалданатын f функциясының графигіне жанама (x0;f(x0)) нүктесі арқылы өтетін және f’(x0) көлбеуі бар қандай да бір түзу болады.

Тангенс теңдеуі

А(x0; f(x0)) нүктесіндегі кейбір f функциясының графигіне жанаманың теңдеуін алуға тырысайық. Еңісі k болатын түзудің теңдеуі келесі түрде болады:

Біздің көлбеуіміз туындыға тең болғандықтан f'(x0), онда теңдеу келесі пішінді алады: y = f'(x0)*x + b.

Енді b мәнін есептейік. Ол үшін функцияның А нүктесі арқылы өту фактісін қолданамыз.

f(x0) = f’(x0)*x0 + b, осы жерден b өрнектеп, b = f(x0) - f’(x0)*x0 аламыз.

Алынған мәнді тангенс теңдеуіне ауыстырамыз:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f'(x0)*(x - x0).

Келесі мысалды қарастырыңыз: x \u003d 2 нүктесіндегі f (x) \u003d x 3 - 2 * x 2 + 1 функциясының графигіне жанаманың теңдеуін табыңыз.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Алынған мәндерді тангенс формуласына ауыстырыңыз, біз мынаны аламыз: y = 1 + 4*(x - 2). Жақшаларды ашып, ұқсас мүшелерді келтірсек, біз мынаны аламыз: y = 4*x - 7.

Жауабы: у = 4*х - 7.

Тангенс теңдеуін құрудың жалпы схемасы y = f(x) функциясының графигіне:

1. x0 мәнін анықтаңыз.

2. f(x0) мәнін есептеңдер.

3. f'(x) есептеңіз